| L(s) = 1 | + 9·3-s + 15·5-s + 21·7-s + 54·9-s + 36·11-s + 50·13-s + 135·15-s + 46·17-s + 76·19-s + 189·21-s + 48·23-s + 150·25-s + 270·27-s + 42·29-s + 80·31-s + 324·33-s + 315·35-s + 130·37-s + 450·39-s + 206·41-s + 148·43-s + 810·45-s + 312·47-s + 294·49-s + 414·51-s + 82·53-s + 540·55-s + ⋯ |
| L(s) = 1 | + 1.73·3-s + 1.34·5-s + 1.13·7-s + 2·9-s + 0.986·11-s + 1.06·13-s + 2.32·15-s + 0.656·17-s + 0.917·19-s + 1.96·21-s + 0.435·23-s + 6/5·25-s + 1.92·27-s + 0.268·29-s + 0.463·31-s + 1.70·33-s + 1.52·35-s + 0.577·37-s + 1.84·39-s + 0.784·41-s + 0.524·43-s + 2.68·45-s + 0.968·47-s + 6/7·49-s + 1.13·51-s + 0.212·53-s + 1.32·55-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{9} \cdot 3^{3} \cdot 5^{3} \cdot 7^{3}\right)^{s/2} \, \Gamma_{\C}(s)^{3} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{9} \cdot 3^{3} \cdot 5^{3} \cdot 7^{3}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{3} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(33.47974281\) |
| \(L(\frac12)\) |
\(\approx\) |
\(33.47974281\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_1$ | \( ( 1 - p T )^{3} \) |
| 5 | $C_1$ | \( ( 1 - p T )^{3} \) |
| 7 | $C_1$ | \( ( 1 - p T )^{3} \) |
| good | 11 | $S_4\times C_2$ | \( 1 - 36 T + 1945 T^{2} - 29272 T^{3} + 1945 p^{3} T^{4} - 36 p^{6} T^{5} + p^{9} T^{6} \) |
| 13 | $S_4\times C_2$ | \( 1 - 50 T + 4571 T^{2} - 231596 T^{3} + 4571 p^{3} T^{4} - 50 p^{6} T^{5} + p^{9} T^{6} \) |
| 17 | $S_4\times C_2$ | \( 1 - 46 T + 655 p T^{2} - 494788 T^{3} + 655 p^{4} T^{4} - 46 p^{6} T^{5} + p^{9} T^{6} \) |
| 19 | $S_4\times C_2$ | \( 1 - 4 p T + 10657 T^{2} - 664968 T^{3} + 10657 p^{3} T^{4} - 4 p^{7} T^{5} + p^{9} T^{6} \) |
| 23 | $S_4\times C_2$ | \( 1 - 48 T + 6037 T^{2} + 1215328 T^{3} + 6037 p^{3} T^{4} - 48 p^{6} T^{5} + p^{9} T^{6} \) |
| 29 | $S_4\times C_2$ | \( 1 - 42 T + 42523 T^{2} + 273572 T^{3} + 42523 p^{3} T^{4} - 42 p^{6} T^{5} + p^{9} T^{6} \) |
| 31 | $S_4\times C_2$ | \( 1 - 80 T + 53069 T^{2} - 4145248 T^{3} + 53069 p^{3} T^{4} - 80 p^{6} T^{5} + p^{9} T^{6} \) |
| 37 | $S_4\times C_2$ | \( 1 - 130 T + 87619 T^{2} - 17340684 T^{3} + 87619 p^{3} T^{4} - 130 p^{6} T^{5} + p^{9} T^{6} \) |
| 41 | $S_4\times C_2$ | \( 1 - 206 T + 119191 T^{2} - 21180004 T^{3} + 119191 p^{3} T^{4} - 206 p^{6} T^{5} + p^{9} T^{6} \) |
| 43 | $S_4\times C_2$ | \( 1 - 148 T + 79849 T^{2} - 32681400 T^{3} + 79849 p^{3} T^{4} - 148 p^{6} T^{5} + p^{9} T^{6} \) |
| 47 | $S_4\times C_2$ | \( 1 - 312 T + 1187 p T^{2} + 9403248 T^{3} + 1187 p^{4} T^{4} - 312 p^{6} T^{5} + p^{9} T^{6} \) |
| 53 | $S_4\times C_2$ | \( 1 - 82 T + 432931 T^{2} - 24524300 T^{3} + 432931 p^{3} T^{4} - 82 p^{6} T^{5} + p^{9} T^{6} \) |
| 59 | $S_4\times C_2$ | \( 1 - 140 T + 611257 T^{2} - 56636552 T^{3} + 611257 p^{3} T^{4} - 140 p^{6} T^{5} + p^{9} T^{6} \) |
| 61 | $S_4\times C_2$ | \( 1 - 186 T + 468091 T^{2} - 38798780 T^{3} + 468091 p^{3} T^{4} - 186 p^{6} T^{5} + p^{9} T^{6} \) |
| 67 | $S_4\times C_2$ | \( 1 - 284 T + 924865 T^{2} - 171168552 T^{3} + 924865 p^{3} T^{4} - 284 p^{6} T^{5} + p^{9} T^{6} \) |
| 71 | $S_4\times C_2$ | \( 1 - 408 T + 355317 T^{2} - 85866960 T^{3} + 355317 p^{3} T^{4} - 408 p^{6} T^{5} + p^{9} T^{6} \) |
| 73 | $S_4\times C_2$ | \( 1 - 526 T + 845415 T^{2} - 272020548 T^{3} + 845415 p^{3} T^{4} - 526 p^{6} T^{5} + p^{9} T^{6} \) |
| 79 | $S_4\times C_2$ | \( 1 - 560 T + 1424141 T^{2} - 516357536 T^{3} + 1424141 p^{3} T^{4} - 560 p^{6} T^{5} + p^{9} T^{6} \) |
| 83 | $S_4\times C_2$ | \( 1 - 532 T + 1044369 T^{2} - 546774136 T^{3} + 1044369 p^{3} T^{4} - 532 p^{6} T^{5} + p^{9} T^{6} \) |
| 89 | $S_4\times C_2$ | \( 1 + 290 T + 1396871 T^{2} + 91121276 T^{3} + 1396871 p^{3} T^{4} + 290 p^{6} T^{5} + p^{9} T^{6} \) |
| 97 | $S_4\times C_2$ | \( 1 - 966 T + 1668639 T^{2} - 1030002036 T^{3} + 1668639 p^{3} T^{4} - 966 p^{6} T^{5} + p^{9} T^{6} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{6} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
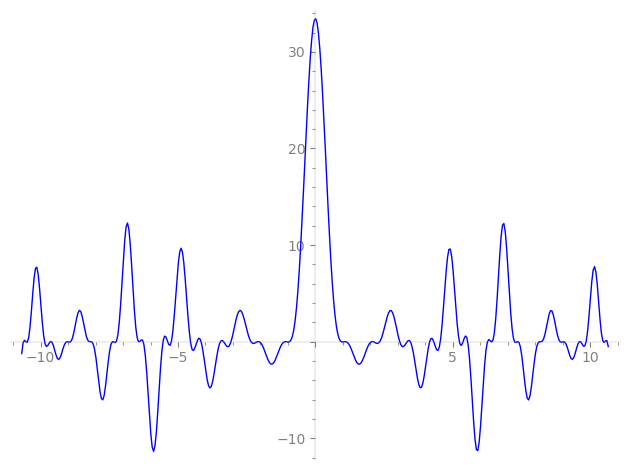
Imaginary part of the first few zeros on the critical line
−8.907102570155231724248824440769, −8.219678213782658979875444503428, −8.201624900276620113345246649641, −8.153510079652835912024203905211, −7.38952215891922055695273872235, −7.35012003383801084611765699053, −7.24850517743019244331101945764, −6.43803935200224102090336047481, −6.39539384909651075093870728014, −6.26512947174865048293319098260, −5.54539934941575614308838802552, −5.37684549817871760474386736200, −5.24146983952263406711900088139, −4.54658213582042936655246265990, −4.30983386522487061692798696791, −4.15863602921226023396879697096, −3.45819762244441066719549883892, −3.34039844502593419929834299413, −3.07072179155660708397194562767, −2.34392394858515759912306937355, −2.10605051742502155071264931165, −2.04183886718977439924273423517, −1.10684467759532670477466266840, −1.06905368473126568155796932574, −0.939811580025310816576548353677,
0.939811580025310816576548353677, 1.06905368473126568155796932574, 1.10684467759532670477466266840, 2.04183886718977439924273423517, 2.10605051742502155071264931165, 2.34392394858515759912306937355, 3.07072179155660708397194562767, 3.34039844502593419929834299413, 3.45819762244441066719549883892, 4.15863602921226023396879697096, 4.30983386522487061692798696791, 4.54658213582042936655246265990, 5.24146983952263406711900088139, 5.37684549817871760474386736200, 5.54539934941575614308838802552, 6.26512947174865048293319098260, 6.39539384909651075093870728014, 6.43803935200224102090336047481, 7.24850517743019244331101945764, 7.35012003383801084611765699053, 7.38952215891922055695273872235, 8.153510079652835912024203905211, 8.201624900276620113345246649641, 8.219678213782658979875444503428, 8.907102570155231724248824440769