| L(s) = 1 | − 2-s − 3-s + 4-s + 6-s − 8-s + 9-s − 3·11-s − 12-s + 16-s − 6·17-s − 18-s + 3·22-s + 9·23-s + 24-s − 27-s − 7·29-s − 31-s − 32-s + 3·33-s + 6·34-s + 36-s − 37-s − 13·43-s − 3·44-s − 9·46-s − 11·47-s − 48-s + ⋯ |
| L(s) = 1 | − 0.707·2-s − 0.577·3-s + 1/2·4-s + 0.408·6-s − 0.353·8-s + 1/3·9-s − 0.904·11-s − 0.288·12-s + 1/4·16-s − 1.45·17-s − 0.235·18-s + 0.639·22-s + 1.87·23-s + 0.204·24-s − 0.192·27-s − 1.29·29-s − 0.179·31-s − 0.176·32-s + 0.522·33-s + 1.02·34-s + 1/6·36-s − 0.164·37-s − 1.98·43-s − 0.452·44-s − 1.32·46-s − 1.60·47-s − 0.144·48-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 25350 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 25350 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.3919217051\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.3919217051\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | \( 1 + T \) | |
| 3 | \( 1 + T \) | |
| 5 | \( 1 \) | |
| 13 | \( 1 \) | |
| good | 7 | \( 1 + p T^{2} \) | 1.7.a |
| 11 | \( 1 + 3 T + p T^{2} \) | 1.11.d |
| 17 | \( 1 + 6 T + p T^{2} \) | 1.17.g |
| 19 | \( 1 + p T^{2} \) | 1.19.a |
| 23 | \( 1 - 9 T + p T^{2} \) | 1.23.aj |
| 29 | \( 1 + 7 T + p T^{2} \) | 1.29.h |
| 31 | \( 1 + T + p T^{2} \) | 1.31.b |
| 37 | \( 1 + T + p T^{2} \) | 1.37.b |
| 41 | \( 1 + p T^{2} \) | 1.41.a |
| 43 | \( 1 + 13 T + p T^{2} \) | 1.43.n |
| 47 | \( 1 + 11 T + p T^{2} \) | 1.47.l |
| 53 | \( 1 + 6 T + p T^{2} \) | 1.53.g |
| 59 | \( 1 - 11 T + p T^{2} \) | 1.59.al |
| 61 | \( 1 + p T^{2} \) | 1.61.a |
| 67 | \( 1 + 4 T + p T^{2} \) | 1.67.e |
| 71 | \( 1 + 4 T + p T^{2} \) | 1.71.e |
| 73 | \( 1 + p T^{2} \) | 1.73.a |
| 79 | \( 1 - T + p T^{2} \) | 1.79.ab |
| 83 | \( 1 + 4 T + p T^{2} \) | 1.83.e |
| 89 | \( 1 - 4 T + p T^{2} \) | 1.89.ae |
| 97 | \( 1 - 4 T + p T^{2} \) | 1.97.ae |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
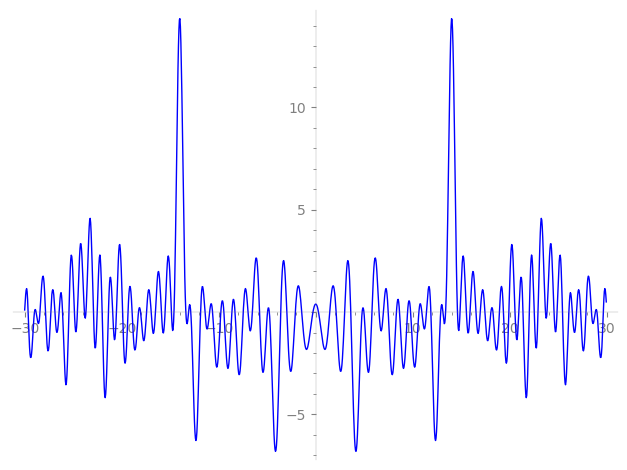
Imaginary part of the first few zeros on the critical line
−15.52555170271522, −14.87582281965249, −14.60748932894453, −13.39193485267997, −13.10973409247152, −12.87597281103552, −11.87083273033114, −11.41627641737128, −10.94116347171543, −10.63196731710394, −9.780667588140672, −9.466797061996460, −8.641448727040072, −8.317438211650341, −7.473405254616341, −6.975075936045564, −6.528914811311842, −5.792615770859560, −4.968741059839864, −4.783317143993853, −3.612781044875497, −2.978416387941668, −2.103385938892142, −1.443049424854020, −0.2858137733752167,
0.2858137733752167, 1.443049424854020, 2.103385938892142, 2.978416387941668, 3.612781044875497, 4.783317143993853, 4.968741059839864, 5.792615770859560, 6.528914811311842, 6.975075936045564, 7.473405254616341, 8.317438211650341, 8.641448727040072, 9.466797061996460, 9.780667588140672, 10.63196731710394, 10.94116347171543, 11.41627641737128, 11.87083273033114, 12.87597281103552, 13.10973409247152, 13.39193485267997, 14.60748932894453, 14.87582281965249, 15.52555170271522