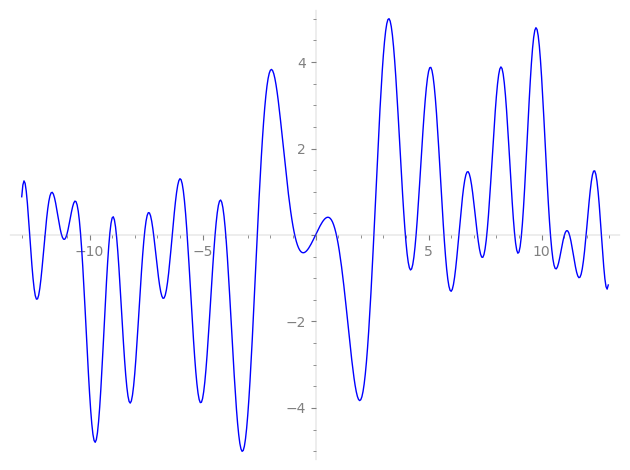
| L(s) = 1 | − 2-s − 2.46·3-s + 4-s − 3.19·5-s + 2.46·6-s − 7-s − 8-s + 3.07·9-s + 3.19·10-s + 1.63·11-s − 2.46·12-s + 14-s + 7.87·15-s + 16-s − 3.38·17-s − 3.07·18-s − 5.90·19-s − 3.19·20-s + 2.46·21-s − 1.63·22-s + 6.07·23-s + 2.46·24-s + 5.19·25-s − 0.179·27-s − 28-s − 0.769·29-s − 7.87·30-s + ⋯ |
| L(s) = 1 | − 0.707·2-s − 1.42·3-s + 0.5·4-s − 1.42·5-s + 1.00·6-s − 0.377·7-s − 0.353·8-s + 1.02·9-s + 1.00·10-s + 0.494·11-s − 0.711·12-s + 0.267·14-s + 2.03·15-s + 0.250·16-s − 0.821·17-s − 0.724·18-s − 1.35·19-s − 0.714·20-s + 0.537·21-s − 0.349·22-s + 1.26·23-s + 0.503·24-s + 1.03·25-s − 0.0346·27-s − 0.188·28-s − 0.142·29-s − 1.43·30-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2366 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2366 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 + T \) |
| 7 | \( 1 + T \) |
| 13 | \( 1 \) |
| good | 3 | \( 1 + 2.46T + 3T^{2} \) |
| 5 | \( 1 + 3.19T + 5T^{2} \) |
| 11 | \( 1 - 1.63T + 11T^{2} \) |
| 17 | \( 1 + 3.38T + 17T^{2} \) |
| 19 | \( 1 + 5.90T + 19T^{2} \) |
| 23 | \( 1 - 6.07T + 23T^{2} \) |
| 29 | \( 1 + 0.769T + 29T^{2} \) |
| 31 | \( 1 + 8.79T + 31T^{2} \) |
| 37 | \( 1 - 8.07T + 37T^{2} \) |
| 41 | \( 1 - 10.5T + 41T^{2} \) |
| 43 | \( 1 - 10.2T + 43T^{2} \) |
| 47 | \( 1 - 8.70T + 47T^{2} \) |
| 53 | \( 1 - 3.75T + 53T^{2} \) |
| 59 | \( 1 - 8.61T + 59T^{2} \) |
| 61 | \( 1 - 1.62T + 61T^{2} \) |
| 67 | \( 1 + 6.49T + 67T^{2} \) |
| 71 | \( 1 + 14.7T + 71T^{2} \) |
| 73 | \( 1 + 16.0T + 73T^{2} \) |
| 79 | \( 1 - 4.98T + 79T^{2} \) |
| 83 | \( 1 - 13.1T + 83T^{2} \) |
| 89 | \( 1 + 13.1T + 89T^{2} \) |
| 97 | \( 1 - 7.70T + 97T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.810786308638672367046743284044, −7.57443068832440792066110531016, −7.16326598755700161388613309962, −6.34028517772382784246492722406, −5.68071061381945066945926689682, −4.44688800781819870736921581646, −3.97286148942958535098352945613, −2.57966245958481391575150125918, −0.922008000786412814647670393604, 0,
0.922008000786412814647670393604, 2.57966245958481391575150125918, 3.97286148942958535098352945613, 4.44688800781819870736921581646, 5.68071061381945066945926689682, 6.34028517772382784246492722406, 7.16326598755700161388613309962, 7.57443068832440792066110531016, 8.810786308638672367046743284044