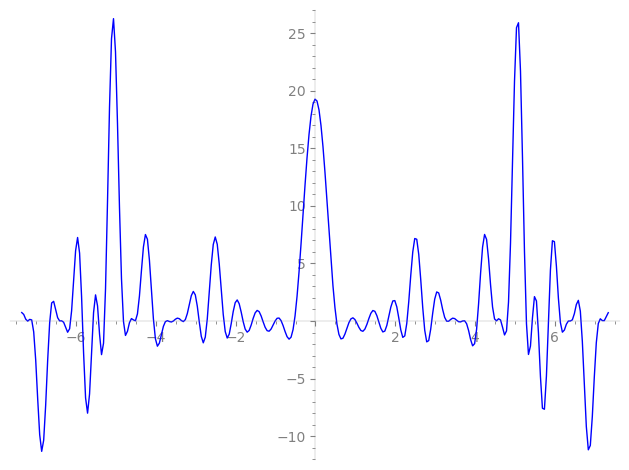
| L(s) = 1 | + 2·3-s + 9-s + 12·11-s + 4·13-s − 4·17-s + 12·19-s + 2·23-s − 2·27-s + 2·29-s + 24·33-s + 8·39-s − 4·43-s − 49-s − 8·51-s + 12·53-s + 24·57-s − 6·59-s − 12·67-s + 4·69-s + 8·79-s − 4·81-s + 4·87-s + 30·89-s + 24·97-s + 12·99-s − 10·101-s + 32·103-s + ⋯ |
| L(s) = 1 | + 1.15·3-s + 1/3·9-s + 3.61·11-s + 1.10·13-s − 0.970·17-s + 2.75·19-s + 0.417·23-s − 0.384·27-s + 0.371·29-s + 4.17·33-s + 1.28·39-s − 0.609·43-s − 1/7·49-s − 1.12·51-s + 1.64·53-s + 3.17·57-s − 0.781·59-s − 1.46·67-s + 0.481·69-s + 0.900·79-s − 4/9·81-s + 0.428·87-s + 3.17·89-s + 2.43·97-s + 1.20·99-s − 0.995·101-s + 3.15·103-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(19.29969424\) |
| \(L(\frac12)\) |
\(\approx\) |
\(19.29969424\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 5 | | \( 1 \) |
| 13 | $C_2$ | \( ( 1 - 2 T + p T^{2} )^{2} \) |
| good | 7 | $C_2^3$ | \( 1 + T^{2} - 48 T^{4} + p^{2} T^{6} + p^{4} T^{8} \) |
| 11 | $C_2^2$ | \( ( 1 - 6 T + 23 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 17 | $C_2^2$ | \( ( 1 + 2 T - 13 T^{2} + 2 p T^{3} + p^{2} T^{4} )^{2} \) |
| 19 | $D_4\times C_2$ | \( 1 - 12 T + 85 T^{2} - 444 T^{3} + 1920 T^{4} - 444 p T^{5} + 85 p^{2} T^{6} - 12 p^{3} T^{7} + p^{4} T^{8} \) |
| 23 | $D_4\times C_2$ | \( 1 - 2 T - 4 T^{2} + 76 T^{3} - 557 T^{4} + 76 p T^{5} - 4 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 - 2 T - 16 T^{2} + 76 T^{3} - 557 T^{4} + 76 p T^{5} - 16 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 31 | $C_2^2$ | \( ( 1 - 50 T^{2} + p^{2} T^{4} )^{2} \) |
| 37 | $C_2^3$ | \( 1 + 22 T^{2} - 885 T^{4} + 22 p^{2} T^{6} + p^{4} T^{8} \) |
| 41 | $C_2^3$ | \( 1 + 30 T^{2} - 781 T^{4} + 30 p^{2} T^{6} + p^{4} T^{8} \) |
| 43 | $D_4\times C_2$ | \( 1 + 4 T - 35 T^{2} - 140 T^{3} + 64 T^{4} - 140 p T^{5} - 35 p^{2} T^{6} + 4 p^{3} T^{7} + p^{4} T^{8} \) |
| 47 | $D_4\times C_2$ | \( 1 - 60 T^{2} + 2822 T^{4} - 60 p^{2} T^{6} + p^{4} T^{8} \) |
| 53 | $D_{4}$ | \( ( 1 - 6 T + 76 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) |
| 59 | $D_4\times C_2$ | \( 1 + 6 T + 120 T^{2} + 648 T^{3} + 8891 T^{4} + 648 p T^{5} + 120 p^{2} T^{6} + 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 61 | $C_2^2$ | \( ( 1 - p T^{2} + p^{2} T^{4} )^{2} \) |
| 67 | $D_4\times C_2$ | \( 1 + 12 T + 181 T^{2} + 1596 T^{3} + 16416 T^{4} + 1596 p T^{5} + 181 p^{2} T^{6} + 12 p^{3} T^{7} + p^{4} T^{8} \) |
| 71 | $C_2^3$ | \( 1 + 90 T^{2} + 3059 T^{4} + 90 p^{2} T^{6} + p^{4} T^{8} \) |
| 73 | $D_4\times C_2$ | \( 1 - 134 T^{2} + 9531 T^{4} - 134 p^{2} T^{6} + p^{4} T^{8} \) |
| 79 | $D_{4}$ | \( ( 1 - 4 T + 123 T^{2} - 4 p T^{3} + p^{2} T^{4} )^{2} \) |
| 83 | $D_4\times C_2$ | \( 1 - 156 T^{2} + 15962 T^{4} - 156 p^{2} T^{6} + p^{4} T^{8} \) |
| 89 | $D_4\times C_2$ | \( 1 - 30 T + 540 T^{2} - 7200 T^{3} + 76379 T^{4} - 7200 p T^{5} + 540 p^{2} T^{6} - 30 p^{3} T^{7} + p^{4} T^{8} \) |
| 97 | $D_4\times C_2$ | \( 1 - 24 T + 382 T^{2} - 4560 T^{3} + 45315 T^{4} - 4560 p T^{5} + 382 p^{2} T^{6} - 24 p^{3} T^{7} + p^{4} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.13451077319336202919969970738, −5.83950456787539991927882425177, −5.57353754195369550090485231395, −5.43337145651644936142373180649, −5.28616711828422478759366636937, −4.81210552683912633712722483073, −4.64889425366845004493025217479, −4.52985107605234308808467850620, −4.52070857630871986092747980356, −4.05700397491470310566691427774, −3.74643817594934564790417892542, −3.68607946367377846121704671086, −3.56099765250542611599915827905, −3.34632605266378184913671718659, −3.28391614473231065689905687459, −2.91435332397011508110545355556, −2.71582596218028871523663029543, −2.29514807043844945756617553056, −2.10063805179919829771050186379, −1.81476195397015990036862464011, −1.58110061320830699687935302325, −1.31806537034984929389841644211, −1.01148987536702612976291608543, −0.856852889143251763721400613337, −0.52765537550494954833769815309,
0.52765537550494954833769815309, 0.856852889143251763721400613337, 1.01148987536702612976291608543, 1.31806537034984929389841644211, 1.58110061320830699687935302325, 1.81476195397015990036862464011, 2.10063805179919829771050186379, 2.29514807043844945756617553056, 2.71582596218028871523663029543, 2.91435332397011508110545355556, 3.28391614473231065689905687459, 3.34632605266378184913671718659, 3.56099765250542611599915827905, 3.68607946367377846121704671086, 3.74643817594934564790417892542, 4.05700397491470310566691427774, 4.52070857630871986092747980356, 4.52985107605234308808467850620, 4.64889425366845004493025217479, 4.81210552683912633712722483073, 5.28616711828422478759366636937, 5.43337145651644936142373180649, 5.57353754195369550090485231395, 5.83950456787539991927882425177, 6.13451077319336202919969970738