| L(s) = 1 | + 4-s − 2·25-s + 4·37-s − 2·49-s − 64-s + 4·73-s + 8·97-s − 2·100-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 4·148-s + 149-s + 151-s + 157-s + 163-s + 167-s + 4·169-s + 173-s + 179-s + 181-s + 191-s + 193-s − 2·196-s + 197-s + ⋯ |
| L(s) = 1 | + 4-s − 2·25-s + 4·37-s − 2·49-s − 64-s + 4·73-s + 8·97-s − 2·100-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 4·148-s + 149-s + 151-s + 157-s + 163-s + 167-s + 4·169-s + 173-s + 179-s + 181-s + 191-s + 193-s − 2·196-s + 197-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{8} \cdot 5^{4} \cdot 17^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{8} \cdot 5^{4} \cdot 17^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(2.275584652\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.275584652\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 3 | | \( 1 \) |
| 5 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 17 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| good | 7 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 13 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 19 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 23 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 29 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 31 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 37 | $C_2$ | \( ( 1 - T + T^{2} )^{4} \) |
| 41 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 53 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 59 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 61 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 67 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 71 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 73 | $C_2$ | \( ( 1 - T + T^{2} )^{4} \) |
| 79 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 83 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 89 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 97 | $C_1$ | \( ( 1 - T )^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
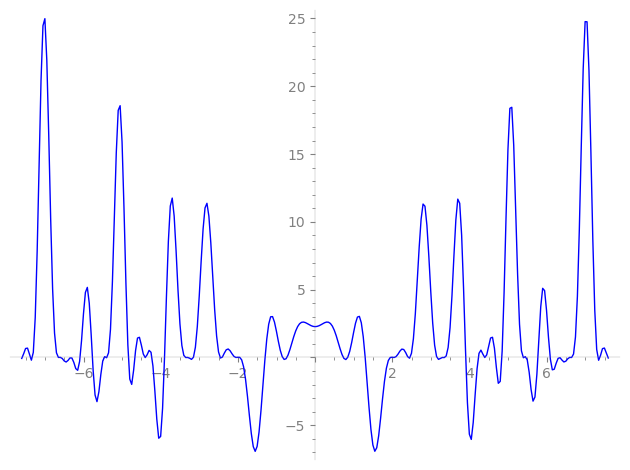
Imaginary part of the first few zeros on the critical line
−6.33615064160918905693715941232, −6.32041258064570606742703428673, −6.09172233355623735808037189683, −5.77200630210502821766733501849, −5.47652898052592435173951243812, −5.41654733324207956637616027723, −5.38792415865690286501318212056, −4.83931807368135081164108041712, −4.67181723668410525451256016283, −4.41038152157346200698053659538, −4.39591132441276826980295838258, −4.22835325781777421176803895892, −3.90320711118705001842637449802, −3.35952140652443165811548227600, −3.32410350612720905936795808011, −3.29395871587091763986623443310, −3.15561432751149715016526089691, −2.46313942033455290578544138059, −2.41091746044873683634890746417, −2.04869352039478789667375482548, −2.03420700972137316577041719758, −1.94672089265550425950176923159, −1.29714422490747276994877955202, −0.842772196439055554428653416484, −0.73131495015754342134099393108,
0.73131495015754342134099393108, 0.842772196439055554428653416484, 1.29714422490747276994877955202, 1.94672089265550425950176923159, 2.03420700972137316577041719758, 2.04869352039478789667375482548, 2.41091746044873683634890746417, 2.46313942033455290578544138059, 3.15561432751149715016526089691, 3.29395871587091763986623443310, 3.32410350612720905936795808011, 3.35952140652443165811548227600, 3.90320711118705001842637449802, 4.22835325781777421176803895892, 4.39591132441276826980295838258, 4.41038152157346200698053659538, 4.67181723668410525451256016283, 4.83931807368135081164108041712, 5.38792415865690286501318212056, 5.41654733324207956637616027723, 5.47652898052592435173951243812, 5.77200630210502821766733501849, 6.09172233355623735808037189683, 6.32041258064570606742703428673, 6.33615064160918905693715941232