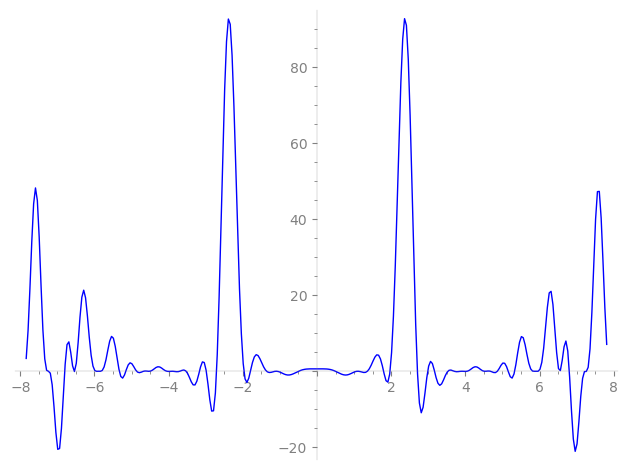
| L(s) = 1 | − 4·4-s + 4·11-s + 10·16-s − 16·44-s − 20·64-s − 2·81-s + 10·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s − 4·169-s + 173-s + 40·176-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + 223-s + ⋯ |
| L(s) = 1 | − 4·4-s + 4·11-s + 10·16-s − 16·44-s − 20·64-s − 2·81-s + 10·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s − 4·169-s + 173-s + 40·176-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + 223-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(5^{4} \cdot 7^{8} \cdot 11^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(5^{4} \cdot 7^{8} \cdot 11^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.6312079524\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.6312079524\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 5 | $C_2^2$ | \( 1 + T^{4} \) |
| 7 | | \( 1 \) |
| 11 | $C_1$ | \( ( 1 - T )^{4} \) |
| good | 2 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 3 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 13 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 17 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 19 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 23 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 29 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 31 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 37 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 41 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 43 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 53 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 59 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 61 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 67 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 71 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 73 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 79 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 83 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 89 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 97 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.53278265704406801652803483653, −5.95679550659563316996676152085, −5.91614494601810307457925902616, −5.85564417915981255348376469200, −5.83724863881151475200761709874, −5.32814233635495795724881399718, −5.15479823618965008461977416085, −4.86142284460666945842415933186, −4.67927151123453615533498238786, −4.54603430815816946420208008426, −4.51440452672631642573194625329, −4.04328241244751956080561598198, −3.93623538959308585142100434302, −3.87834555979006430906335924929, −3.70186479719869404843653232243, −3.52730270832621748606188294582, −3.16902753606273088822438170271, −2.98484281570796194382828405835, −2.70782101406624975259688814205, −1.96939761677621951081599274363, −1.79502511493818856227222277876, −1.35732832162976737532460029248, −1.12356069103734399541537193762, −1.07577267783576213340749759037, −0.49869158035286412600577071118,
0.49869158035286412600577071118, 1.07577267783576213340749759037, 1.12356069103734399541537193762, 1.35732832162976737532460029248, 1.79502511493818856227222277876, 1.96939761677621951081599274363, 2.70782101406624975259688814205, 2.98484281570796194382828405835, 3.16902753606273088822438170271, 3.52730270832621748606188294582, 3.70186479719869404843653232243, 3.87834555979006430906335924929, 3.93623538959308585142100434302, 4.04328241244751956080561598198, 4.51440452672631642573194625329, 4.54603430815816946420208008426, 4.67927151123453615533498238786, 4.86142284460666945842415933186, 5.15479823618965008461977416085, 5.32814233635495795724881399718, 5.83724863881151475200761709874, 5.85564417915981255348376469200, 5.91614494601810307457925902616, 5.95679550659563316996676152085, 6.53278265704406801652803483653