↑

Properties

Label 2-12e3-24.11-c3-0-63
Degree $2$
Conductor $1728$
Sign $0.965 + 0.258i$
Analytic cond. $101.955$
Root an. cond. $10.0972$
Motivic weight $3$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 8.20·5-s + 10.6i·7-s − 61.3i·11-s + 46.7i·13-s − 23.7i·17-s + 145.·19-s + 57.4·23-s − 57.6·25-s − 48.8·29-s + 247. i·31-s + 87.3i·35-s − 71.1i·37-s − 394. i·41-s + 158.·43-s − 478.·47-s + ⋯
L(s)  = 1  + 0.734·5-s + 0.574i·7-s − 1.68i·11-s + 0.996i·13-s − 0.338i·17-s + 1.75·19-s + 0.520·23-s − 0.460·25-s − 0.312·29-s + 1.43i·31-s + 0.422i·35-s − 0.316i·37-s − 1.50i·41-s + 0.560·43-s − 1.48·47-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1728 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.965 + 0.258i)\, \overline{\Lambda}(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1728 ^{s/2} \, \Gamma_{\C}(s+3/2) \, L(s)\cr =\mathstrut & (0.965 + 0.258i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1728\)    =    \(2^{6} \cdot 3^{3}\)
Sign: $0.965 + 0.258i$
Analytic conductor: \(101.955\)
Root analytic conductor: \(10.0972\)
Motivic weight: \(3\)
Rational: no
Arithmetic: yes
Character: $\chi_{1728} (863, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1728,\ (\ :3/2),\ 0.965 + 0.258i)\)

Particular Values

\(L(2)\) \(\approx\) \(2.676608903\)
\(L(\frac12)\) \(\approx\) \(2.676608903\)
\(L(\frac{5}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
3 \( 1 \)
good5 \( 1 - 8.20T + 125T^{2} \)
7 \( 1 - 10.6iT - 343T^{2} \)
11 \( 1 + 61.3iT - 1.33e3T^{2} \)
13 \( 1 - 46.7iT - 2.19e3T^{2} \)
17 \( 1 + 23.7iT - 4.91e3T^{2} \)
19 \( 1 - 145.T + 6.85e3T^{2} \)
23 \( 1 - 57.4T + 1.21e4T^{2} \)
29 \( 1 + 48.8T + 2.43e4T^{2} \)
31 \( 1 - 247. iT - 2.97e4T^{2} \)
37 \( 1 + 71.1iT - 5.06e4T^{2} \)
41 \( 1 + 394. iT - 6.89e4T^{2} \)
43 \( 1 - 158.T + 7.95e4T^{2} \)
47 \( 1 + 478.T + 1.03e5T^{2} \)
53 \( 1 - 273.T + 1.48e5T^{2} \)
59 \( 1 - 355. iT - 2.05e5T^{2} \)
61 \( 1 + 810. iT - 2.26e5T^{2} \)
67 \( 1 + 240.T + 3.00e5T^{2} \)
71 \( 1 - 985.T + 3.57e5T^{2} \)
73 \( 1 - 416.T + 3.89e5T^{2} \)
79 \( 1 - 659. iT - 4.93e5T^{2} \)
83 \( 1 + 493. iT - 5.71e5T^{2} \)
89 \( 1 + 302. iT - 7.04e5T^{2} \)
97 \( 1 - 537.T + 9.12e5T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

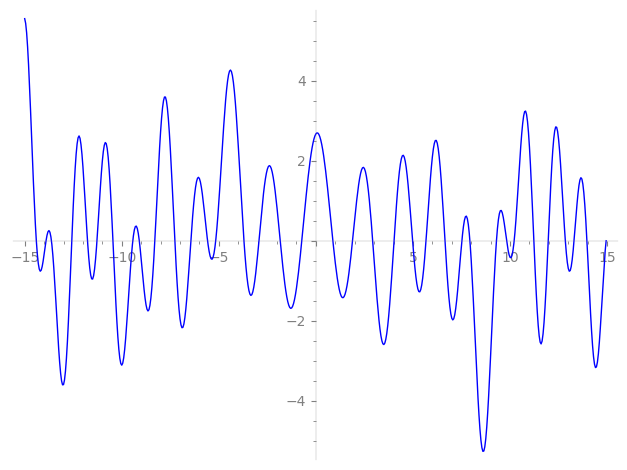
Imaginary part of the first few zeros on the critical line

−9.096094110658910713847574323084, −8.297606783682329011205572036523, −7.26502301869215024480832901380, −6.44068540916970070715573380085, −5.57860926157161685488285186305, −5.16227404222040648585816647386, −3.70541031040378865373686739256, −2.93415126378480068522521742430, −1.83675297905081185171996469623, −0.72813303412994323837595858286, 0.874762093808147299415982869166, 1.88560641760973181208501550027, 2.92553801412417396982615051969, 4.02417519138790786231738497659, 4.98028489567259108002289897525, 5.67030954426865973208558942023, 6.64918198864202798760044439018, 7.51857000819058185534662789367, 7.932385713051405660830185356264, 9.299274755773469645675745518752

Graph of the $Z$-function along the critical line