↑

Properties

Label 8-150e4-1.1-c13e4-0-2
Degree $8$
Conductor $506250000$
Sign $1$
Analytic cond. $6.69337\times 10^{8}$
Root an. cond. $12.6825$
Motivic weight $13$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 8.19e3·4-s − 1.06e6·9-s + 1.19e7·11-s + 5.03e7·16-s − 4.71e8·19-s + 3.96e9·29-s − 7.19e9·31-s + 8.70e9·36-s + 2.15e10·41-s − 9.79e10·44-s + 2.41e11·49-s + 6.57e11·59-s + 1.97e12·61-s − 2.74e11·64-s + 5.25e12·71-s + 3.86e12·76-s − 1.02e13·79-s + 8.47e11·81-s − 2.17e13·89-s − 1.27e13·99-s + 2.64e13·101-s − 4.79e13·109-s − 3.24e13·116-s − 3.10e13·121-s + 5.89e13·124-s + 127-s + 131-s + ⋯
L(s)  = 1  − 4-s − 2/3·9-s + 2.03·11-s + 3/4·16-s − 2.30·19-s + 1.23·29-s − 1.45·31-s + 2/3·36-s + 0.709·41-s − 2.03·44-s + 2.49·49-s + 2.02·59-s + 4.91·61-s − 1/2·64-s + 4.87·71-s + 2.30·76-s − 4.72·79-s + 1/3·81-s − 4.64·89-s − 1.35·99-s + 2.48·101-s − 2.73·109-s − 1.23·116-s − 0.899·121-s + 1.45·124-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{4} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(14-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{4} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s+13/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]

Invariants

Degree: \(8\)
Conductor: \(2^{4} \cdot 3^{4} \cdot 5^{8}\)
Sign: $1$
Analytic conductor: \(6.69337\times 10^{8}\)
Root analytic conductor: \(12.6825\)
Motivic weight: \(13\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((8,\ 2^{4} \cdot 3^{4} \cdot 5^{8} ,\ ( \ : 13/2, 13/2, 13/2, 13/2 ),\ 1 )\)

Particular Values

\(L(7)\) \(\approx\) \(0.9290212962\)
\(L(\frac12)\) \(\approx\) \(0.9290212962\)
\(L(\frac{15}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad2$C_2$ \( ( 1 + p^{12} T^{2} )^{2} \)
3$C_2$ \( ( 1 + p^{12} T^{2} )^{2} \)
5 \( 1 \)
good7$D_4\times C_2$ \( 1 - 241595360810 T^{2} + \)\(68\!\cdots\!27\)\( p^{2} T^{4} - 241595360810 p^{26} T^{6} + p^{52} T^{8} \)
11$D_{4}$ \( ( 1 - 543564 p T + 571556717146 p^{2} T^{2} - 543564 p^{14} T^{3} + p^{26} T^{4} )^{2} \)
13$D_4\times C_2$ \( 1 - 231788791013570 T^{2} - \)\(89\!\cdots\!57\)\( T^{4} - 231788791013570 p^{26} T^{6} + p^{52} T^{8} \)
17$D_4\times C_2$ \( 1 - 10585771841811740 T^{2} + \)\(19\!\cdots\!38\)\( T^{4} - 10585771841811740 p^{26} T^{6} + p^{52} T^{8} \)
19$D_{4}$ \( ( 1 + 235842370 T + 68417795789105943 T^{2} + 235842370 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
23$D_4\times C_2$ \( 1 - 1002495082838338100 T^{2} + \)\(54\!\cdots\!78\)\( T^{4} - 1002495082838338100 p^{26} T^{6} + p^{52} T^{8} \)
29$D_{4}$ \( ( 1 - 1982573220 T + 5122619844605044078 T^{2} - 1982573220 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
31$D_{4}$ \( ( 1 + 3595146506 T + 14316134264262207591 T^{2} + 3595146506 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
37$D_4\times C_2$ \( 1 - \)\(69\!\cdots\!00\)\( T^{2} + \)\(23\!\cdots\!18\)\( T^{4} - \)\(69\!\cdots\!00\)\( p^{26} T^{6} + p^{52} T^{8} \)
41$D_{4}$ \( ( 1 - 10794170904 T + \)\(17\!\cdots\!46\)\( T^{2} - 10794170904 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
43$D_4\times C_2$ \( 1 - \)\(50\!\cdots\!70\)\( T^{2} + \)\(12\!\cdots\!23\)\( T^{4} - \)\(50\!\cdots\!70\)\( p^{26} T^{6} + p^{52} T^{8} \)
47$D_4\times C_2$ \( 1 - \)\(17\!\cdots\!20\)\( T^{2} + \)\(13\!\cdots\!58\)\( T^{4} - \)\(17\!\cdots\!20\)\( p^{26} T^{6} + p^{52} T^{8} \)
53$D_4\times C_2$ \( 1 - \)\(40\!\cdots\!60\)\( T^{2} + \)\(85\!\cdots\!58\)\( T^{4} - \)\(40\!\cdots\!60\)\( p^{26} T^{6} + p^{52} T^{8} \)
59$D_{4}$ \( ( 1 - 328627140780 T + \)\(22\!\cdots\!58\)\( T^{2} - 328627140780 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
61$D_{4}$ \( ( 1 - 989162363254 T + \)\(51\!\cdots\!91\)\( T^{2} - 989162363254 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
67$D_4\times C_2$ \( 1 - \)\(20\!\cdots\!30\)\( T^{2} + \)\(16\!\cdots\!63\)\( T^{4} - \)\(20\!\cdots\!30\)\( p^{26} T^{6} + p^{52} T^{8} \)
71$D_{4}$ \( ( 1 - 2629674680664 T + \)\(38\!\cdots\!46\)\( T^{2} - 2629674680664 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
73$D_4\times C_2$ \( 1 - \)\(26\!\cdots\!00\)\( T^{2} + \)\(62\!\cdots\!78\)\( T^{4} - \)\(26\!\cdots\!00\)\( p^{26} T^{6} + p^{52} T^{8} \)
79$D_{4}$ \( ( 1 + 5109552231280 T + \)\(13\!\cdots\!78\)\( T^{2} + 5109552231280 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
83$D_4\times C_2$ \( 1 - \)\(33\!\cdots\!60\)\( T^{2} + \)\(43\!\cdots\!38\)\( T^{4} - \)\(33\!\cdots\!60\)\( p^{26} T^{6} + p^{52} T^{8} \)
89$D_{4}$ \( ( 1 + 10899866035680 T + \)\(72\!\cdots\!38\)\( T^{2} + 10899866035680 p^{13} T^{3} + p^{26} T^{4} )^{2} \)
97$D_4\times C_2$ \( 1 - \)\(11\!\cdots\!70\)\( T^{2} + \)\(90\!\cdots\!83\)\( T^{4} - \)\(11\!\cdots\!70\)\( p^{26} T^{6} + p^{52} T^{8} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

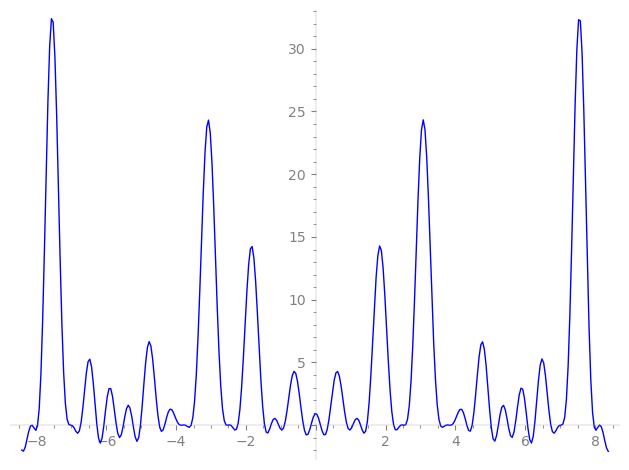
Imaginary part of the first few zeros on the critical line

−7.01778825720110275462934851368, −7.01477402418503796553537338074, −6.73338593285059125252847134017, −6.26806494000300350396268595143, −6.06833111686468750775859277843, −5.71150374679172690303035326241, −5.51109124589768791551403144667, −5.23077841594208087259279703428, −5.02089492305847831549704528718, −4.48012748589652471026949115881, −4.32755033418447625059234556399, −3.88010913867326704877467938211, −3.82372430207192990986325736132, −3.73585943939500932467234651955, −3.56844490579942271298234099676, −2.56328244181267694896083834147, −2.51254088795644306126035277897, −2.43573266295297670712789182765, −2.23251761888813496246379419768, −1.46484143796707659905974421778, −1.28466757967830769187509286947, −1.06085486972939136081634916534, −0.896365769112155196958612095086, −0.35278812894125799970452229204, −0.13624238182852039020254171291, 0.13624238182852039020254171291, 0.35278812894125799970452229204, 0.896365769112155196958612095086, 1.06085486972939136081634916534, 1.28466757967830769187509286947, 1.46484143796707659905974421778, 2.23251761888813496246379419768, 2.43573266295297670712789182765, 2.51254088795644306126035277897, 2.56328244181267694896083834147, 3.56844490579942271298234099676, 3.73585943939500932467234651955, 3.82372430207192990986325736132, 3.88010913867326704877467938211, 4.32755033418447625059234556399, 4.48012748589652471026949115881, 5.02089492305847831549704528718, 5.23077841594208087259279703428, 5.51109124589768791551403144667, 5.71150374679172690303035326241, 6.06833111686468750775859277843, 6.26806494000300350396268595143, 6.73338593285059125252847134017, 7.01477402418503796553537338074, 7.01778825720110275462934851368

Graph of the $Z$-function along the critical line