| L(s) = 1 | − 12·3-s − 8·5-s − 10·7-s + 90·9-s − 74·11-s + 58·13-s + 96·15-s + 66·17-s + 76·19-s + 120·21-s + 34·23-s − 61·25-s − 540·27-s + 308·29-s − 302·31-s + 888·33-s + 80·35-s + 122·37-s − 696·39-s + 400·41-s + 74·43-s − 720·45-s − 628·47-s − 349·49-s − 792·51-s + 504·53-s + 592·55-s + ⋯ |
| L(s) = 1 | − 2.30·3-s − 0.715·5-s − 0.539·7-s + 10/3·9-s − 2.02·11-s + 1.23·13-s + 1.65·15-s + 0.941·17-s + 0.917·19-s + 1.24·21-s + 0.308·23-s − 0.487·25-s − 3.84·27-s + 1.97·29-s − 1.74·31-s + 4.68·33-s + 0.386·35-s + 0.542·37-s − 2.85·39-s + 1.52·41-s + 0.262·43-s − 2.38·45-s − 1.94·47-s − 1.01·49-s − 2.17·51-s + 1.30·53-s + 1.45·55-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 19^{4}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_1$ | \( ( 1 + p T )^{4} \) |
| 19 | $C_1$ | \( ( 1 - p T )^{4} \) |
| good | 5 | $C_2 \wr S_4$ | \( 1 + 8 T + p^{3} T^{2} + 2142 T^{3} + 3896 p T^{4} + 2142 p^{3} T^{5} + p^{9} T^{6} + 8 p^{9} T^{7} + p^{12} T^{8} \) |
| 7 | $C_2 \wr S_4$ | \( 1 + 10 T + 449 T^{2} - 46 p T^{3} + 54860 T^{4} - 46 p^{4} T^{5} + 449 p^{6} T^{6} + 10 p^{9} T^{7} + p^{12} T^{8} \) |
| 11 | $C_2 \wr S_4$ | \( 1 + 74 T + 6453 T^{2} + 284230 T^{3} + 13542412 T^{4} + 284230 p^{3} T^{5} + 6453 p^{6} T^{6} + 74 p^{9} T^{7} + p^{12} T^{8} \) |
| 13 | $C_2 \wr S_4$ | \( 1 - 58 T + 9240 T^{2} - 382014 T^{3} + 30946974 T^{4} - 382014 p^{3} T^{5} + 9240 p^{6} T^{6} - 58 p^{9} T^{7} + p^{12} T^{8} \) |
| 17 | $C_2 \wr S_4$ | \( 1 - 66 T + 10189 T^{2} - 536606 T^{3} + 60584484 T^{4} - 536606 p^{3} T^{5} + 10189 p^{6} T^{6} - 66 p^{9} T^{7} + p^{12} T^{8} \) |
| 23 | $C_2 \wr S_4$ | \( 1 - 34 T + 8644 T^{2} - 509866 T^{3} + 276283094 T^{4} - 509866 p^{3} T^{5} + 8644 p^{6} T^{6} - 34 p^{9} T^{7} + p^{12} T^{8} \) |
| 29 | $C_2 \wr S_4$ | \( 1 - 308 T + 96868 T^{2} - 15852156 T^{3} + 3097364454 T^{4} - 15852156 p^{3} T^{5} + 96868 p^{6} T^{6} - 308 p^{9} T^{7} + p^{12} T^{8} \) |
| 31 | $C_2 \wr S_4$ | \( 1 + 302 T + 61528 T^{2} + 1452030 T^{3} - 3162126 p T^{4} + 1452030 p^{3} T^{5} + 61528 p^{6} T^{6} + 302 p^{9} T^{7} + p^{12} T^{8} \) |
| 37 | $C_2 \wr S_4$ | \( 1 - 122 T + 58156 T^{2} + 4245578 T^{3} - 116529562 T^{4} + 4245578 p^{3} T^{5} + 58156 p^{6} T^{6} - 122 p^{9} T^{7} + p^{12} T^{8} \) |
| 41 | $C_2 \wr S_4$ | \( 1 - 400 T + 128016 T^{2} - 20682896 T^{3} + 5025752254 T^{4} - 20682896 p^{3} T^{5} + 128016 p^{6} T^{6} - 400 p^{9} T^{7} + p^{12} T^{8} \) |
| 43 | $C_2 \wr S_4$ | \( 1 - 74 T + 84521 T^{2} + 7996270 T^{3} + 3670108564 T^{4} + 7996270 p^{3} T^{5} + 84521 p^{6} T^{6} - 74 p^{9} T^{7} + p^{12} T^{8} \) |
| 47 | $C_2 \wr S_4$ | \( 1 + 628 T + 479033 T^{2} + 174712550 T^{3} + 74596509492 T^{4} + 174712550 p^{3} T^{5} + 479033 p^{6} T^{6} + 628 p^{9} T^{7} + p^{12} T^{8} \) |
| 53 | $C_2 \wr S_4$ | \( 1 - 504 T + 460268 T^{2} - 180089384 T^{3} + 91371291190 T^{4} - 180089384 p^{3} T^{5} + 460268 p^{6} T^{6} - 504 p^{9} T^{7} + p^{12} T^{8} \) |
| 59 | $C_2 \wr S_4$ | \( 1 + 1036 T + 857452 T^{2} + 404394540 T^{3} + 208960015990 T^{4} + 404394540 p^{3} T^{5} + 857452 p^{6} T^{6} + 1036 p^{9} T^{7} + p^{12} T^{8} \) |
| 61 | $C_2 \wr S_4$ | \( 1 + 422 T + 677625 T^{2} + 195523902 T^{3} + 200968547420 T^{4} + 195523902 p^{3} T^{5} + 677625 p^{6} T^{6} + 422 p^{9} T^{7} + p^{12} T^{8} \) |
| 67 | $C_2 \wr S_4$ | \( 1 + 336 T + 874764 T^{2} + 217642640 T^{3} + 364058731990 T^{4} + 217642640 p^{3} T^{5} + 874764 p^{6} T^{6} + 336 p^{9} T^{7} + p^{12} T^{8} \) |
| 71 | $C_2 \wr S_4$ | \( 1 + 348 T + 586732 T^{2} + 153198284 T^{3} + 150984030278 T^{4} + 153198284 p^{3} T^{5} + 586732 p^{6} T^{6} + 348 p^{9} T^{7} + p^{12} T^{8} \) |
| 73 | $C_2 \wr S_4$ | \( 1 + 182 T + 520305 T^{2} + 136384466 T^{3} + 111255730780 T^{4} + 136384466 p^{3} T^{5} + 520305 p^{6} T^{6} + 182 p^{9} T^{7} + p^{12} T^{8} \) |
| 79 | $C_2 \wr S_4$ | \( 1 + 1402 T + 785652 T^{2} - 490280814 T^{3} - 689718890922 T^{4} - 490280814 p^{3} T^{5} + 785652 p^{6} T^{6} + 1402 p^{9} T^{7} + p^{12} T^{8} \) |
| 83 | $C_2 \wr S_4$ | \( 1 + 2392 T + 4020412 T^{2} + 4326122584 T^{3} + 3827911778614 T^{4} + 4326122584 p^{3} T^{5} + 4020412 p^{6} T^{6} + 2392 p^{9} T^{7} + p^{12} T^{8} \) |
| 89 | $C_2 \wr S_4$ | \( 1 + 288 T + 2060572 T^{2} + 619730144 T^{3} + 1984443769958 T^{4} + 619730144 p^{3} T^{5} + 2060572 p^{6} T^{6} + 288 p^{9} T^{7} + p^{12} T^{8} \) |
| 97 | $C_2 \wr S_4$ | \( 1 + 1816 T + 2909340 T^{2} + 2384967528 T^{3} + 2576444206662 T^{4} + 2384967528 p^{3} T^{5} + 2909340 p^{6} T^{6} + 1816 p^{9} T^{7} + p^{12} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
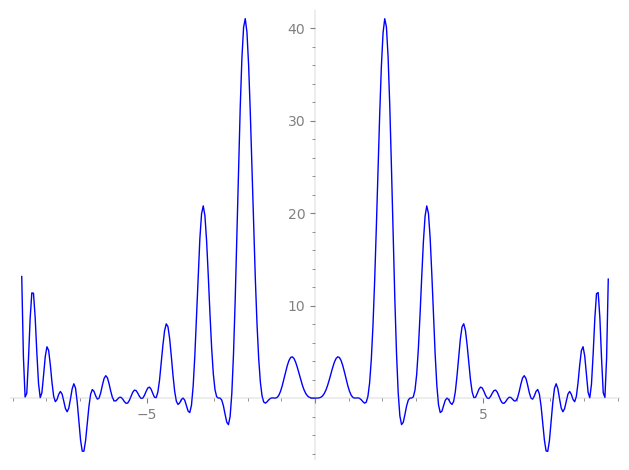
Imaginary part of the first few zeros on the critical line
−7.27141056477849398021499328130, −7.08667359803467036421342227922, −6.69545501111481684447563122936, −6.49806843596426375253365582609, −6.42463140611504651139292895870, −6.02119738743573443501592791210, −5.84887662192841163664451917564, −5.74479250272617352128304391895, −5.49466984016673202674555162915, −5.18756186890168681658221124260, −5.12308749335312714464990278260, −4.75240483393066724678462792040, −4.74043827103190835782473520994, −4.14566108993432192491776969816, −3.93386990991409903431755764148, −3.92201779878107358491987206123, −3.65284308846261177471640798694, −2.87960333120579657408312339891, −2.87601238958042683103791551261, −2.81933643314737162674122428640, −2.48340313569323796516873384050, −1.56315374647345944296507501082, −1.30838084707214348559409071429, −1.20616648309545438651402151266, −1.17386047175275935980877988329, 0, 0, 0, 0,
1.17386047175275935980877988329, 1.20616648309545438651402151266, 1.30838084707214348559409071429, 1.56315374647345944296507501082, 2.48340313569323796516873384050, 2.81933643314737162674122428640, 2.87601238958042683103791551261, 2.87960333120579657408312339891, 3.65284308846261177471640798694, 3.92201779878107358491987206123, 3.93386990991409903431755764148, 4.14566108993432192491776969816, 4.74043827103190835782473520994, 4.75240483393066724678462792040, 5.12308749335312714464990278260, 5.18756186890168681658221124260, 5.49466984016673202674555162915, 5.74479250272617352128304391895, 5.84887662192841163664451917564, 6.02119738743573443501592791210, 6.42463140611504651139292895870, 6.49806843596426375253365582609, 6.69545501111481684447563122936, 7.08667359803467036421342227922, 7.27141056477849398021499328130