| L(s) = 1 | + 23·4-s − 28·9-s − 172·11-s + 273·16-s − 332·19-s − 240·29-s − 156·31-s − 644·36-s − 144·41-s − 3.95e3·44-s − 344·49-s − 36·59-s + 1.76e3·61-s + 1.86e3·64-s + 1.26e3·71-s − 7.63e3·76-s + 360·79-s − 870·81-s + 1.70e3·89-s + 4.81e3·99-s − 1.43e3·101-s − 2.00e3·109-s − 5.52e3·116-s + 1.32e4·121-s − 3.58e3·124-s + 127-s + 131-s + ⋯ |
| L(s) = 1 | + 23/8·4-s − 1.03·9-s − 4.71·11-s + 4.26·16-s − 4.00·19-s − 1.53·29-s − 0.903·31-s − 2.98·36-s − 0.548·41-s − 13.5·44-s − 1.00·49-s − 0.0794·59-s + 3.71·61-s + 3.63·64-s + 2.11·71-s − 11.5·76-s + 0.512·79-s − 1.19·81-s + 2.02·89-s + 4.88·99-s − 1.41·101-s − 1.76·109-s − 4.41·116-s + 9.91·121-s − 2.59·124-s + 0.000698·127-s + 0.000666·131-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(1.138318708\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.138318708\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 5 | | \( 1 \) |
| 13 | $C_2$ | \( ( 1 + p^{2} T^{2} )^{2} \) |
| good | 2 | $D_4\times C_2$ | \( 1 - 23 T^{2} + p^{8} T^{4} - 23 p^{6} T^{6} + p^{12} T^{8} \) |
| 3 | $C_2^2$ | \( ( 1 + 14 T^{2} + p^{6} T^{4} )^{2} \) |
| 7 | $D_4\times C_2$ | \( 1 + 344 T^{2} + 207694 T^{4} + 344 p^{6} T^{6} + p^{12} T^{8} \) |
| 11 | $D_{4}$ | \( ( 1 + 86 T + 4494 T^{2} + 86 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 17 | $D_4\times C_2$ | \( 1 - 10556 T^{2} + 72720454 T^{4} - 10556 p^{6} T^{6} + p^{12} T^{8} \) |
| 19 | $D_{4}$ | \( ( 1 + 166 T + 18550 T^{2} + 166 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 23 | $D_4\times C_2$ | \( 1 - 524 p T^{2} + 269715654 T^{4} - 524 p^{7} T^{6} + p^{12} T^{8} \) |
| 29 | $D_{4}$ | \( ( 1 + 120 T + 49046 T^{2} + 120 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 31 | $D_{4}$ | \( ( 1 + 78 T - 6370 T^{2} + 78 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 37 | $D_4\times C_2$ | \( 1 - 126796 T^{2} + 8436922422 T^{4} - 126796 p^{6} T^{6} + p^{12} T^{8} \) |
| 41 | $D_{4}$ | \( ( 1 + 72 T + 73790 T^{2} + 72 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 43 | $D_4\times C_2$ | \( 1 - 303460 T^{2} + 35651554198 T^{4} - 303460 p^{6} T^{6} + p^{12} T^{8} \) |
| 47 | $D_4\times C_2$ | \( 1 - 317096 T^{2} + 44555033134 T^{4} - 317096 p^{6} T^{6} + p^{12} T^{8} \) |
| 53 | $D_4\times C_2$ | \( 1 - 438764 T^{2} + 86315015094 T^{4} - 438764 p^{6} T^{6} + p^{12} T^{8} \) |
| 59 | $D_{4}$ | \( ( 1 + 18 T + 282166 T^{2} + 18 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 61 | $C_2$ | \( ( 1 - 442 T + p^{3} T^{2} )^{4} \) |
| 67 | $D_4\times C_2$ | \( 1 + 45640 T^{2} - 146122156962 T^{4} + 45640 p^{6} T^{6} + p^{12} T^{8} \) |
| 71 | $D_{4}$ | \( ( 1 - 634 T + 397278 T^{2} - 634 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 73 | $D_4\times C_2$ | \( 1 - 594652 T^{2} + 389343894054 T^{4} - 594652 p^{6} T^{6} + p^{12} T^{8} \) |
| 79 | $D_{4}$ | \( ( 1 - 180 T + 993566 T^{2} - 180 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 83 | $D_4\times C_2$ | \( 1 - 1628296 T^{2} + 1213750645950 T^{4} - 1628296 p^{6} T^{6} + p^{12} T^{8} \) |
| 89 | $D_{4}$ | \( ( 1 - 852 T + 1530214 T^{2} - 852 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 97 | $D_4\times C_2$ | \( 1 + 2290436 T^{2} + 2974426681990 T^{4} + 2290436 p^{6} T^{6} + p^{12} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
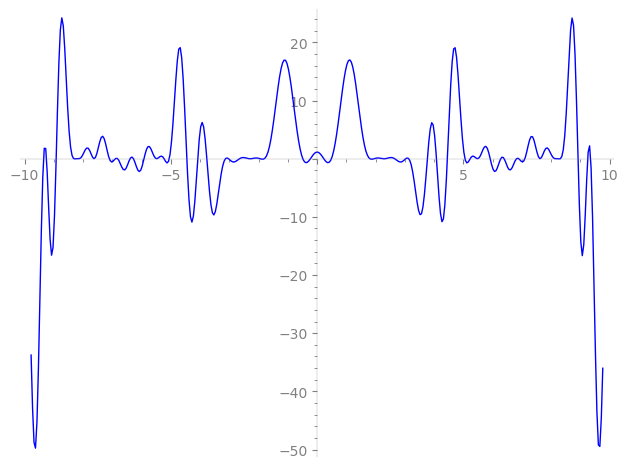
Imaginary part of the first few zeros on the critical line
−8.150591127862362749051870063942, −7.62759326969094039406532574322, −7.62422430152429718988456763772, −7.10563133339860375452582719594, −6.89727074695931173133426326957, −6.82173456867997246230694191276, −6.39600827508622411533346037847, −6.28051374851687058742028141414, −5.91938440011778565118135270875, −5.48809667409390659055116116946, −5.48589894511406454913312404391, −5.23391558015119175413089245744, −5.05594185050115871998939385649, −4.45443838445958258044302562530, −4.08170195147836979093341666490, −3.77134612938288975070328446811, −3.13416266728827836970972209449, −3.03176666626076553117189387990, −2.65173580761558458183699484979, −2.31923059261535261809190180376, −2.26006530379529034969869267922, −1.95127736316067166352825301833, −1.80418180991444037869452657697, −0.48992907040486426228021143251, −0.22707981122104294905158700584,
0.22707981122104294905158700584, 0.48992907040486426228021143251, 1.80418180991444037869452657697, 1.95127736316067166352825301833, 2.26006530379529034969869267922, 2.31923059261535261809190180376, 2.65173580761558458183699484979, 3.03176666626076553117189387990, 3.13416266728827836970972209449, 3.77134612938288975070328446811, 4.08170195147836979093341666490, 4.45443838445958258044302562530, 5.05594185050115871998939385649, 5.23391558015119175413089245744, 5.48589894511406454913312404391, 5.48809667409390659055116116946, 5.91938440011778565118135270875, 6.28051374851687058742028141414, 6.39600827508622411533346037847, 6.82173456867997246230694191276, 6.89727074695931173133426326957, 7.10563133339860375452582719594, 7.62422430152429718988456763772, 7.62759326969094039406532574322, 8.150591127862362749051870063942