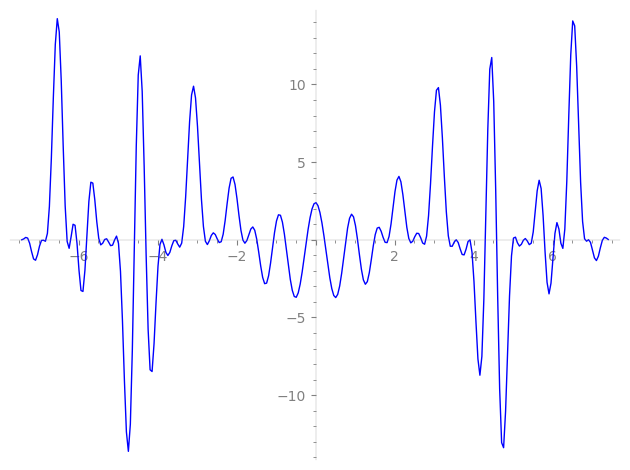
| L(s) = 1 | + 2·4-s − 5·16-s + 16·19-s − 28·31-s + 26·49-s − 4·61-s − 20·64-s + 32·76-s + 40·79-s − 32·109-s − 38·121-s − 56·124-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s − 2·169-s + 173-s + 179-s + 181-s + 191-s + 193-s + ⋯ |
| L(s) = 1 | + 4-s − 5/4·16-s + 3.67·19-s − 5.02·31-s + 26/7·49-s − 0.512·61-s − 5/2·64-s + 3.67·76-s + 4.50·79-s − 3.06·109-s − 3.45·121-s − 5.02·124-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s − 0.153·169-s + 0.0760·173-s + 0.0747·179-s + 0.0743·181-s + 0.0723·191-s + 0.0719·193-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{8} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{8} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(2.398186088\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.398186088\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 3 | | \( 1 \) | |
| 5 | | \( 1 \) | |
| 13 | $C_2$ | \( ( 1 + T^{2} )^{2} \) | |
| good | 2 | $C_2^2$ | \( ( 1 - T^{2} + p^{2} T^{4} )^{2} \) | 4.2.a_ac_a_j |
| 7 | $C_2^2$ | \( ( 1 - 13 T^{2} + p^{2} T^{4} )^{2} \) | 4.7.a_aba_a_kh |
| 11 | $C_2^2$ | \( ( 1 + 19 T^{2} + p^{2} T^{4} )^{2} \) | 4.11.a_bm_a_xf |
| 17 | $C_2^2$ | \( ( 1 - 31 T^{2} + p^{2} T^{4} )^{2} \) | 4.17.a_ack_a_chf |
| 19 | $C_2$ | \( ( 1 - 4 T + p T^{2} )^{4} \) | 4.19.aq_gq_absy_izm |
| 23 | $C_2^2$ | \( ( 1 - 34 T^{2} + p^{2} T^{4} )^{2} \) | 4.23.a_acq_a_dhe |
| 29 | $C_2^2$ | \( ( 1 - 17 T^{2} + p^{2} T^{4} )^{2} \) | 4.29.a_abi_a_cxv |
| 31 | $C_2$ | \( ( 1 + 7 T + p T^{2} )^{4} \) | 4.31.bc_qc_fwy_bnbf |
| 37 | $C_2$ | \( ( 1 - 12 T + p T^{2} )^{2}( 1 + 12 T + p T^{2} )^{2} \) | 4.37.a_afk_a_lhu |
| 41 | $C_2^2$ | \( ( 1 + 34 T^{2} + p^{2} T^{4} )^{2} \) | 4.41.a_cq_a_gru |
| 43 | $C_2^2$ | \( ( 1 - 82 T^{2} + p^{2} T^{4} )^{2} \) | 4.43.a_agi_a_pkw |
| 47 | $C_2^2$ | \( ( 1 - 67 T^{2} + p^{2} T^{4} )^{2} \) | 4.47.a_afe_a_nep |
| 53 | $C_2^2$ | \( ( 1 - 79 T^{2} + p^{2} T^{4} )^{2} \) | 4.53.a_agc_a_rod |
| 59 | $C_2^2$ | \( ( 1 + 115 T^{2} + p^{2} T^{4} )^{2} \) | 4.59.a_iw_a_bdwl |
| 61 | $C_2$ | \( ( 1 + T + p T^{2} )^{4} \) | 4.61.e_jq_bci_bicx |
| 67 | $C_2^2$ | \( ( 1 - 109 T^{2} + p^{2} T^{4} )^{2} \) | 4.67.a_aik_a_bewh |
| 71 | $C_2^2$ | \( ( 1 + 130 T^{2} + p^{2} T^{4} )^{2} \) | 4.71.a_ka_a_bnxu |
| 73 | $C_2^2$ | \( ( 1 - 142 T^{2} + p^{2} T^{4} )^{2} \) | 4.73.a_aky_a_btpm |
| 79 | $C_2$ | \( ( 1 - 10 T + p T^{2} )^{4} \) | 4.79.abo_bjg_atym_icla |
| 83 | $C_2^2$ | \( ( 1 - 139 T^{2} + p^{2} T^{4} )^{2} \) | 4.83.a_aks_a_bwzb |
| 89 | $C_2^2$ | \( ( 1 - 14 T^{2} + p^{2} T^{4} )^{2} \) | 4.89.a_abc_a_xsw |
| 97 | $C_2^2$ | \( ( 1 - 94 T^{2} + p^{2} T^{4} )^{2} \) | 4.97.a_ahg_a_boxq |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.19889054535747132481430289966, −6.04642747631276403560297722505, −5.79477077526578424622843245326, −5.48215390350104008243365343631, −5.34452335578449319532398100664, −5.26823559524779129842497467189, −5.08638572823473836100864496713, −5.00213419137796563468951644640, −4.58486862572456010722942950181, −4.29772429341183878234593991363, −3.91047490494637834348969922688, −3.87854528581707752050142689427, −3.56589560308895201485104891059, −3.55474730962531863137403770579, −3.37442240240249635805494681426, −2.79637224912859775866549113796, −2.68005172107787680668098894854, −2.47919152696313631682303128727, −2.37052060568989267025379288309, −1.84083484868013825479855568996, −1.73160248069822715414244624443, −1.48636409206754488166709447275, −1.06341067891492854639025673760, −0.76916814800549889023729251957, −0.22660678315634878167474486895,
0.22660678315634878167474486895, 0.76916814800549889023729251957, 1.06341067891492854639025673760, 1.48636409206754488166709447275, 1.73160248069822715414244624443, 1.84083484868013825479855568996, 2.37052060568989267025379288309, 2.47919152696313631682303128727, 2.68005172107787680668098894854, 2.79637224912859775866549113796, 3.37442240240249635805494681426, 3.55474730962531863137403770579, 3.56589560308895201485104891059, 3.87854528581707752050142689427, 3.91047490494637834348969922688, 4.29772429341183878234593991363, 4.58486862572456010722942950181, 5.00213419137796563468951644640, 5.08638572823473836100864496713, 5.26823559524779129842497467189, 5.34452335578449319532398100664, 5.48215390350104008243365343631, 5.79477077526578424622843245326, 6.04642747631276403560297722505, 6.19889054535747132481430289966