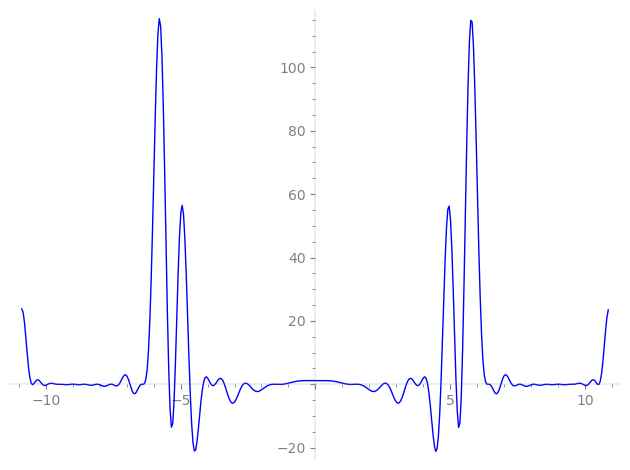
| L(s) = 1 | − 4·2-s + 4·3-s + 8·4-s − 16·6-s − 8·8-s + 8·9-s + 12·11-s + 32·12-s − 4·16-s + 8·17-s − 32·18-s − 48·22-s − 32·24-s + 8·27-s + 32·32-s + 48·33-s − 32·34-s + 64·36-s + 12·41-s − 24·43-s + 96·44-s − 16·48-s + 32·51-s − 32·54-s − 64·64-s − 192·66-s − 12·67-s + ⋯ |
| L(s) = 1 | − 2.82·2-s + 2.30·3-s + 4·4-s − 6.53·6-s − 2.82·8-s + 8/3·9-s + 3.61·11-s + 9.23·12-s − 16-s + 1.94·17-s − 7.54·18-s − 10.2·22-s − 6.53·24-s + 1.53·27-s + 5.65·32-s + 8.35·33-s − 5.48·34-s + 32/3·36-s + 1.87·41-s − 3.65·43-s + 14.4·44-s − 2.30·48-s + 4.48·51-s − 4.35·54-s − 8·64-s − 23.6·66-s − 1.46·67-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 5^{8}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.159457532\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.159457532\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ | Isogeny Class over $\mathbf{F}_p$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + p T + p T^{2} )^{2} \) | |
| 5 | | \( 1 \) | |
| good | 3 | $C_2^3$ | \( 1 - 4 T + 8 T^{2} - 8 T^{3} + 7 T^{4} - 8 p T^{5} + 8 p^{2} T^{6} - 4 p^{3} T^{7} + p^{4} T^{8} \) | 4.3.ae_i_ai_h |
| 7 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.7.a_a_a_du |
| 11 | $C_2^2$ | \( ( 1 - 6 T + 25 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) | 4.11.am_di_aqq_clv |
| 13 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.13.a_a_a_na |
| 17 | $C_2^3$ | \( 1 - 8 T + 32 T^{2} + 16 T^{3} - 353 T^{4} + 16 p T^{5} + 32 p^{2} T^{6} - 8 p^{3} T^{7} + p^{4} T^{8} \) | 4.17.ai_bg_q_anp |
| 19 | $C_2^3$ | \( 1 + 34 T^{2} + 795 T^{4} + 34 p^{2} T^{6} + p^{4} T^{8} \) | 4.19.a_bi_a_bep |
| 23 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.23.a_a_a_bos |
| 29 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) | 4.29.a_em_a_hmc |
| 31 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) | 4.31.a_aeu_a_inu |
| 37 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.37.a_a_a_ebi |
| 41 | $C_2^2$ | \( ( 1 - 6 T - 5 T^{2} - 6 p T^{3} + p^{2} T^{4} )^{2} \) | 4.41.am_ba_aqq_jjv |
| 43 | $C_2^2$ | \( ( 1 + 12 T + 72 T^{2} + 12 p T^{3} + p^{2} T^{4} )^{2} \) | 4.43.y_lc_ece_bfly |
| 47 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.47.a_a_a_gny |
| 53 | $C_2^2$ | \( ( 1 + p^{2} T^{4} )^{2} \) | 4.53.a_a_a_iic |
| 59 | $C_2^2$ | \( ( 1 - 82 T^{2} + p^{2} T^{4} )^{2} \) | 4.59.a_agi_a_ugk |
| 61 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) | 4.61.a_ajk_a_bhas |
| 67 | $C_2^3$ | \( 1 + 12 T + 72 T^{2} - 744 T^{3} - 8953 T^{4} - 744 p T^{5} + 72 p^{2} T^{6} + 12 p^{3} T^{7} + p^{4} T^{8} \) | 4.67.m_cu_abcq_angj |
| 71 | $C_2$ | \( ( 1 - p T^{2} )^{4} \) | 4.71.a_aky_a_bsti |
| 73 | $C_2^3$ | \( 1 - 24 T + 288 T^{2} - 3408 T^{3} + 35567 T^{4} - 3408 p T^{5} + 288 p^{2} T^{6} - 24 p^{3} T^{7} + p^{4} T^{8} \) | 4.73.ay_lc_afbc_capz |
| 79 | $C_2$ | \( ( 1 + p T^{2} )^{4} \) | 4.79.a_me_a_cdkg |
| 83 | $C_2^3$ | \( 1 - 4 T + 8 T^{2} + 632 T^{3} - 8153 T^{4} + 632 p T^{5} + 8 p^{2} T^{6} - 4 p^{3} T^{7} + p^{4} T^{8} \) | 4.83.ae_i_yi_ambp |
| 89 | $C_2^3$ | \( 1 - 146 T^{2} + 13395 T^{4} - 146 p^{2} T^{6} + p^{4} T^{8} \) | 4.89.a_afq_a_tvf |
| 97 | $C_2^2$ | \( ( 1 + 24 T + 288 T^{2} + 24 p T^{3} + p^{2} T^{4} )^{2} \) | 4.97.bw_bsi_bbiu_mdvu |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.075386270305743456111669374471, −8.919035410774494668655604571252, −8.612355657735416625151711212113, −8.530371062815566589764359998436, −8.135353542294709890638399826797, −8.054354402602776235122436829433, −7.61994537890570221415359716884, −7.53642513031176473899114654887, −7.28389756232541699026474306370, −6.87691233178741832768403120483, −6.45768595387331283592302037889, −6.38829663838537002314798036852, −6.38602663613342916368681228413, −5.42371730889517472827306854170, −5.21769434972679527417117987926, −4.65466229978006254095935892279, −4.16201700503382330888923021674, −3.86864348766341949039949940876, −3.71980077277414013329180913973, −3.37353164140908391934862083490, −2.67532738732859170952269144336, −2.49550216379092708987216803478, −1.60057827921239647620794052730, −1.44881509239209763905538121864, −1.23191512801668199079886864908,
1.23191512801668199079886864908, 1.44881509239209763905538121864, 1.60057827921239647620794052730, 2.49550216379092708987216803478, 2.67532738732859170952269144336, 3.37353164140908391934862083490, 3.71980077277414013329180913973, 3.86864348766341949039949940876, 4.16201700503382330888923021674, 4.65466229978006254095935892279, 5.21769434972679527417117987926, 5.42371730889517472827306854170, 6.38602663613342916368681228413, 6.38829663838537002314798036852, 6.45768595387331283592302037889, 6.87691233178741832768403120483, 7.28389756232541699026474306370, 7.53642513031176473899114654887, 7.61994537890570221415359716884, 8.054354402602776235122436829433, 8.135353542294709890638399826797, 8.530371062815566589764359998436, 8.612355657735416625151711212113, 8.919035410774494668655604571252, 9.075386270305743456111669374471