| L(s) = 1 | + 2·3-s + 9-s − 2·13-s + 2·19-s − 2·27-s + 4·31-s − 2·37-s − 4·39-s + 2·43-s + 2·49-s + 4·57-s + 2·73-s − 4·81-s + 8·93-s − 4·97-s + 2·103-s − 4·109-s − 4·111-s − 2·117-s + 127-s + 4·129-s + 131-s + 137-s + 139-s + 4·147-s + 149-s + 151-s + ⋯ |
| L(s) = 1 | + 2·3-s + 9-s − 2·13-s + 2·19-s − 2·27-s + 4·31-s − 2·37-s − 4·39-s + 2·43-s + 2·49-s + 4·57-s + 2·73-s − 4·81-s + 8·93-s − 4·97-s + 2·103-s − 4·109-s − 4·111-s − 2·117-s + 127-s + 4·129-s + 131-s + 137-s + 139-s + 4·147-s + 149-s + 151-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(2.132532005\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.132532005\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 31 | $C_1$ | \( ( 1 - T )^{4} \) |
| good | 5 | $C_2^3$ | \( 1 - T^{4} + T^{8} \) |
| 7 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 11 | $C_2^3$ | \( 1 - T^{4} + T^{8} \) |
| 13 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 17 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 19 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 23 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 29 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 37 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 41 | $C_2^3$ | \( 1 - T^{4} + T^{8} \) |
| 43 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 47 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 53 | $C_2^3$ | \( 1 - T^{4} + T^{8} \) |
| 59 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 61 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 67 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 71 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 73 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 79 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 83 | $C_2^3$ | \( 1 - T^{4} + T^{8} \) |
| 89 | $C_2^2$ | \( ( 1 + T^{4} )^{2} \) |
| 97 | $C_2$ | \( ( 1 + T + T^{2} )^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
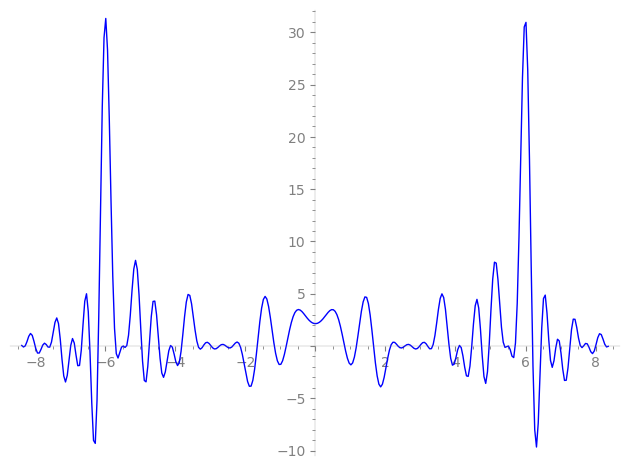
Imaginary part of the first few zeros on the critical line
−6.98862076991237046302970316419, −6.87229986578758896240434500639, −6.67676020691574627698621896683, −6.44336537445637030472902141655, −6.20205067709878527538397755497, −5.70761171693700806983269452152, −5.50941571005153683925693880276, −5.48944336888896938773546287539, −5.39009489689890052340480304046, −4.96141967028226395979456037872, −4.74536578721635215919933043812, −4.46538886779011262927949681678, −4.14557444829591670301149602783, −4.10086759046186615584538793277, −3.81873953914127123248587204921, −3.35093313902389467527853844616, −3.20371737051449272370168600072, −2.97951030655189822603981625199, −2.73957898884315249914658529658, −2.55685208186438792925535687420, −2.35687728200638243264532391716, −2.14926695070671086109540678659, −1.66083765800930797764087294820, −1.17206694885182745879743589511, −0.832594640287397168433054810559,
0.832594640287397168433054810559, 1.17206694885182745879743589511, 1.66083765800930797764087294820, 2.14926695070671086109540678659, 2.35687728200638243264532391716, 2.55685208186438792925535687420, 2.73957898884315249914658529658, 2.97951030655189822603981625199, 3.20371737051449272370168600072, 3.35093313902389467527853844616, 3.81873953914127123248587204921, 4.10086759046186615584538793277, 4.14557444829591670301149602783, 4.46538886779011262927949681678, 4.74536578721635215919933043812, 4.96141967028226395979456037872, 5.39009489689890052340480304046, 5.48944336888896938773546287539, 5.50941571005153683925693880276, 5.70761171693700806983269452152, 6.20205067709878527538397755497, 6.44336537445637030472902141655, 6.67676020691574627698621896683, 6.87229986578758896240434500639, 6.98862076991237046302970316419