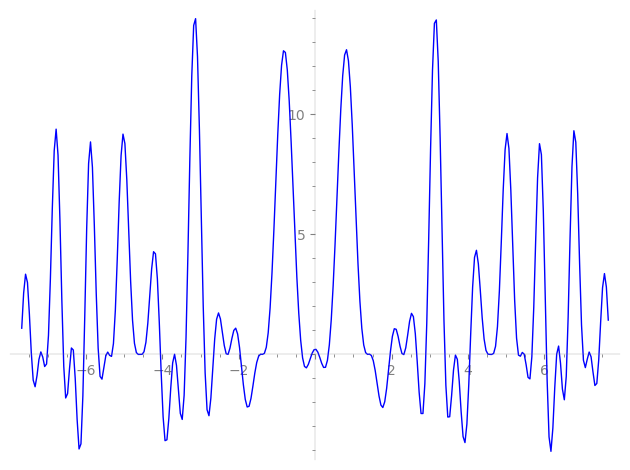
| L(s) = 1 | + 12·7-s − 12·13-s − 60·19-s + 12·25-s − 72·31-s − 28·37-s − 24·43-s + 38·49-s + 52·61-s − 204·67-s + 60·73-s − 324·79-s − 144·91-s − 180·97-s − 84·103-s + 168·109-s + 268·121-s + 127-s + 131-s − 720·133-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + ⋯ |
| L(s) = 1 | + 12/7·7-s − 0.923·13-s − 3.15·19-s + 0.479·25-s − 2.32·31-s − 0.756·37-s − 0.558·43-s + 0.775·49-s + 0.852·61-s − 3.04·67-s + 0.821·73-s − 4.10·79-s − 1.58·91-s − 1.85·97-s − 0.815·103-s + 1.54·109-s + 2.21·121-s + 0.00787·127-s + 0.00763·131-s − 5.41·133-s + 0.00729·137-s + 0.00719·139-s + 0.00671·149-s + 0.00662·151-s + 0.00636·157-s + 0.00613·163-s + 0.00598·167-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{24} \cdot 3^{12}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(3-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{24} \cdot 3^{12}\right)^{s/2} \, \Gamma_{\C}(s+1)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{3}{2})\) |
\(\approx\) |
\(0.2198126333\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.2198126333\) |
| \(L(2)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| good | 5 | $D_4\times C_2$ | \( 1 - 12 T^{2} + 134 T^{4} - 12 p^{4} T^{6} + p^{8} T^{8} \) |
| 7 | $D_{4}$ | \( ( 1 - 6 T + 5 p T^{2} - 6 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 11 | $D_4\times C_2$ | \( 1 - 268 T^{2} + 36870 T^{4} - 268 p^{4} T^{6} + p^{8} T^{8} \) |
| 13 | $D_{4}$ | \( ( 1 + 6 T + 275 T^{2} + 6 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 17 | $D_4\times C_2$ | \( 1 - 1068 T^{2} + 451046 T^{4} - 1068 p^{4} T^{6} + p^{8} T^{8} \) |
| 19 | $D_{4}$ | \( ( 1 + 30 T + 659 T^{2} + 30 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 23 | $D_4\times C_2$ | \( 1 - 172 T^{2} + 582 p^{2} T^{4} - 172 p^{4} T^{6} + p^{8} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 - 3012 T^{2} + 3664166 T^{4} - 3012 p^{4} T^{6} + p^{8} T^{8} \) |
| 31 | $C_2$ | \( ( 1 + 18 T + p^{2} T^{2} )^{4} \) |
| 37 | $D_{4}$ | \( ( 1 + 14 T + 2139 T^{2} + 14 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 41 | $D_4\times C_2$ | \( 1 - 4068 T^{2} + 9622790 T^{4} - 4068 p^{4} T^{6} + p^{8} T^{8} \) |
| 43 | $D_{4}$ | \( ( 1 + 12 T + 2582 T^{2} + 12 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 47 | $D_4\times C_2$ | \( 1 - 1708 T^{2} + 9980646 T^{4} - 1708 p^{4} T^{6} + p^{8} T^{8} \) |
| 53 | $D_4\times C_2$ | \( 1 - 900 T^{2} - 4088986 T^{4} - 900 p^{4} T^{6} + p^{8} T^{8} \) |
| 59 | $D_4\times C_2$ | \( 1 - 5068 T^{2} + 17955078 T^{4} - 5068 p^{4} T^{6} + p^{8} T^{8} \) |
| 61 | $D_{4}$ | \( ( 1 - 26 T + 1779 T^{2} - 26 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 67 | $D_{4}$ | \( ( 1 + 102 T + 10427 T^{2} + 102 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 71 | $D_4\times C_2$ | \( 1 - 9796 T^{2} + 64196934 T^{4} - 9796 p^{4} T^{6} + p^{8} T^{8} \) |
| 73 | $D_{4}$ | \( ( 1 - 30 T + 10595 T^{2} - 30 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 79 | $D_{4}$ | \( ( 1 + 162 T + 18395 T^{2} + 162 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| 83 | $D_4\times C_2$ | \( 1 - 12868 T^{2} + 132165798 T^{4} - 12868 p^{4} T^{6} + p^{8} T^{8} \) |
| 89 | $D_4\times C_2$ | \( 1 - 6060 T^{2} - 29067226 T^{4} - 6060 p^{4} T^{6} + p^{8} T^{8} \) |
| 97 | $D_{4}$ | \( ( 1 + 90 T + 18251 T^{2} + 90 p^{2} T^{3} + p^{4} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.40040475933497421095949300945, −6.31916949241770260290393848156, −6.05301935882843816602580354156, −5.67277695627717199844987655509, −5.47084740816617531592746951103, −5.39211819352405522790173774945, −5.31506216881513899350685394631, −4.63710169090721210480640388344, −4.58858475658697840795497424309, −4.57890418499697644246847896875, −4.53898861635505837198898849152, −4.04929154191672374118865660813, −3.69060306487865981995615840381, −3.67783125921589836839656232448, −3.39271617620134723055169091747, −2.89671301977412894976433864848, −2.65780283478935440118947914592, −2.32294063312547569458962122706, −2.28042170162823266161052955718, −1.96081844252218136198612765274, −1.44363559123825621120762011341, −1.37727480203966989988149955201, −1.36701127164179076805582755977, −0.34265815273615916255227781925, −0.092211804433837282248876264636,
0.092211804433837282248876264636, 0.34265815273615916255227781925, 1.36701127164179076805582755977, 1.37727480203966989988149955201, 1.44363559123825621120762011341, 1.96081844252218136198612765274, 2.28042170162823266161052955718, 2.32294063312547569458962122706, 2.65780283478935440118947914592, 2.89671301977412894976433864848, 3.39271617620134723055169091747, 3.67783125921589836839656232448, 3.69060306487865981995615840381, 4.04929154191672374118865660813, 4.53898861635505837198898849152, 4.57890418499697644246847896875, 4.58858475658697840795497424309, 4.63710169090721210480640388344, 5.31506216881513899350685394631, 5.39211819352405522790173774945, 5.47084740816617531592746951103, 5.67277695627717199844987655509, 6.05301935882843816602580354156, 6.31916949241770260290393848156, 6.40040475933497421095949300945