| L(s) = 1 | + 16·4-s + 140·7-s + 192·16-s + 964·25-s + 2.24e3·28-s − 5.19e3·37-s − 9.70e3·43-s + 9.89e3·49-s + 2.04e3·64-s + 1.27e4·67-s − 7.96e3·79-s + 1.54e4·100-s + 4.05e4·109-s + 2.68e4·112-s − 5.33e4·121-s + 127-s + 131-s + 137-s + 139-s − 8.30e4·148-s + 149-s + 151-s + 157-s + 163-s + 167-s + 5.87e4·169-s − 1.55e5·172-s + ⋯ |
| L(s) = 1 | + 4-s + 20/7·7-s + 3/4·16-s + 1.54·25-s + 20/7·28-s − 3.79·37-s − 5.24·43-s + 4.12·49-s + 1/2·64-s + 2.84·67-s − 1.27·79-s + 1.54·100-s + 3.40·109-s + 15/7·112-s − 3.64·121-s + 6.20e−5·127-s + 5.82e−5·131-s + 5.32e−5·137-s + 5.17e−5·139-s − 3.79·148-s + 4.50e−5·149-s + 4.38e−5·151-s + 4.05e−5·157-s + 3.76e−5·163-s + 3.58e−5·167-s + 2.05·169-s − 5.24·172-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(5-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 7^{4}\right)^{s/2} \, \Gamma_{\C}(s+2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{5}{2})\) |
\(\approx\) |
\(7.039059475\) |
| \(L(\frac12)\) |
\(\approx\) |
\(7.039059475\) |
| \(L(3)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 - p^{3} T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 7 | $C_2$ | \( ( 1 - 10 p T + p^{4} T^{2} )^{2} \) |
| good | 5 | $C_2^2$ | \( ( 1 - 482 T^{2} + p^{8} T^{4} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 + 26690 T^{2} + p^{8} T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 - 29378 T^{2} + p^{8} T^{4} )^{2} \) |
| 17 | $C_2^2$ | \( ( 1 + 29566 T^{2} + p^{8} T^{4} )^{2} \) |
| 19 | $C_2^2$ | \( ( 1 - 251042 T^{2} + p^{8} T^{4} )^{2} \) |
| 23 | $C_2^2$ | \( ( 1 + 226754 T^{2} + p^{8} T^{4} )^{2} \) |
| 29 | $C_2^2$ | \( ( 1 + 778370 T^{2} + p^{8} T^{4} )^{2} \) |
| 31 | $C_2^2$ | \( ( 1 + 1582174 T^{2} + p^{8} T^{4} )^{2} \) |
| 37 | $C_2$ | \( ( 1 + 1298 T + p^{4} T^{2} )^{4} \) |
| 41 | $C_2^2$ | \( ( 1 - 3243074 T^{2} + p^{8} T^{4} )^{2} \) |
| 43 | $C_2$ | \( ( 1 + 2426 T + p^{4} T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 - 8650370 T^{2} + p^{8} T^{4} )^{2} \) |
| 53 | $C_2^2$ | \( ( 1 + 6553154 T^{2} + p^{8} T^{4} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 - 7412450 T^{2} + p^{8} T^{4} )^{2} \) |
| 61 | $C_2^2$ | \( ( 1 - 25014338 T^{2} + p^{8} T^{4} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - 3194 T + p^{4} T^{2} )^{4} \) |
| 71 | $C_2^2$ | \( ( 1 + 48791234 T^{2} + p^{8} T^{4} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 - 55948226 T^{2} + p^{8} T^{4} )^{2} \) |
| 79 | $C_2$ | \( ( 1 + 1990 T + p^{4} T^{2} )^{4} \) |
| 83 | $C_2^2$ | \( ( 1 - 93291554 T^{2} + p^{8} T^{4} )^{2} \) |
| 89 | $C_2^2$ | \( ( 1 + 30035518 T^{2} + p^{8} T^{4} )^{2} \) |
| 97 | $C_2^2$ | \( ( 1 + 85570174 T^{2} + p^{8} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
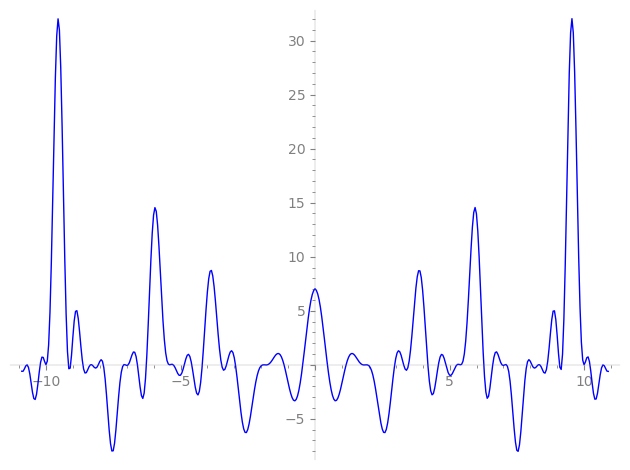
Imaginary part of the first few zeros on the critical line
−9.085614729721988583904390938065, −8.629648778757865482877918651962, −8.350451352923996907563664342687, −8.295093296443235042996909456186, −8.057621138552480439966940482002, −7.86940666062140017159188147414, −7.11557988825374886358015115593, −7.05355292726853771780815282231, −6.94649135050779547524437123409, −6.60269317783100445328150538550, −6.27143605990288574727561044908, −5.41409682596741991198503666958, −5.40184615263926089989620959688, −5.27265579651575827721432328129, −4.86181220213461629305810967029, −4.58312082008877288887474210519, −4.19292223620148556002681991947, −3.47350294935812534757972526532, −3.29227741832146992017511403328, −2.95953044862160638253091311400, −1.91633068703270326228819931261, −1.90569345766633068172148348777, −1.77259235213787723455913742483, −1.15344921786498256338438596314, −0.45954508527249661149609126562,
0.45954508527249661149609126562, 1.15344921786498256338438596314, 1.77259235213787723455913742483, 1.90569345766633068172148348777, 1.91633068703270326228819931261, 2.95953044862160638253091311400, 3.29227741832146992017511403328, 3.47350294935812534757972526532, 4.19292223620148556002681991947, 4.58312082008877288887474210519, 4.86181220213461629305810967029, 5.27265579651575827721432328129, 5.40184615263926089989620959688, 5.41409682596741991198503666958, 6.27143605990288574727561044908, 6.60269317783100445328150538550, 6.94649135050779547524437123409, 7.05355292726853771780815282231, 7.11557988825374886358015115593, 7.86940666062140017159188147414, 8.057621138552480439966940482002, 8.295093296443235042996909456186, 8.350451352923996907563664342687, 8.629648778757865482877918651962, 9.085614729721988583904390938065