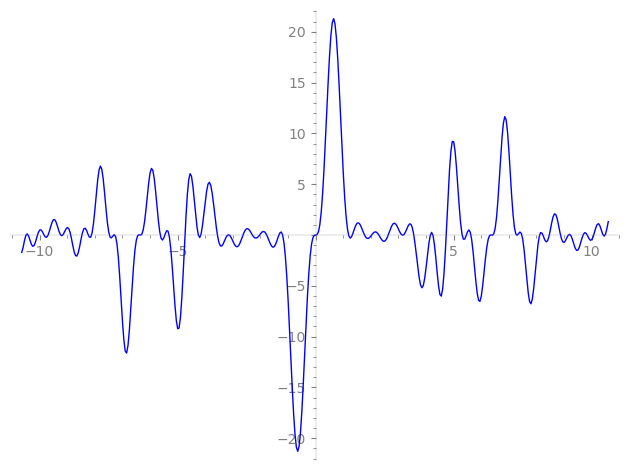
| L(s) = 1 | + 81·3-s + 524·5-s − 722·7-s + 4.37e3·9-s − 6.75e3·11-s + 6.59e3·13-s + 4.24e4·15-s − 1.54e4·17-s − 1.82e3·19-s − 5.84e4·21-s − 1.65e4·23-s + 2.53e4·25-s + 1.96e5·27-s − 1.51e5·29-s − 4.63e4·31-s − 5.46e5·33-s − 3.78e5·35-s − 1.12e5·37-s + 5.33e5·39-s + 3.24e5·41-s − 1.28e6·43-s + 2.29e6·45-s − 9.17e5·47-s − 6.94e5·49-s − 1.24e6·51-s + 2.68e6·53-s − 3.53e6·55-s + ⋯ |
| L(s) = 1 | + 1.73·3-s + 1.87·5-s − 0.795·7-s + 2·9-s − 1.52·11-s + 0.832·13-s + 3.24·15-s − 0.761·17-s − 0.0610·19-s − 1.37·21-s − 0.283·23-s + 0.324·25-s + 1.92·27-s − 1.15·29-s − 0.279·31-s − 2.64·33-s − 1.49·35-s − 0.364·37-s + 1.44·39-s + 0.736·41-s − 2.46·43-s + 3.74·45-s − 1.28·47-s − 0.843·49-s − 1.31·51-s + 2.48·53-s − 2.86·55-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{3} \cdot 13^{3}\right)^{s/2} \, \Gamma_{\C}(s)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(8-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{3} \cdot 13^{3}\right)^{s/2} \, \Gamma_{\C}(s+7/2)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(4)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{9}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_1$ | \( ( 1 - p^{3} T )^{3} \) |
| 13 | $C_1$ | \( ( 1 - p^{3} T )^{3} \) |
| good | 5 | $S_4\times C_2$ | \( 1 - 524 T + 249219 T^{2} - 15787048 p T^{3} + 249219 p^{7} T^{4} - 524 p^{14} T^{5} + p^{21} T^{6} \) |
| 7 | $S_4\times C_2$ | \( 1 + 722 T + 1216277 T^{2} + 1217824796 T^{3} + 1216277 p^{7} T^{4} + 722 p^{14} T^{5} + p^{21} T^{6} \) |
| 11 | $S_4\times C_2$ | \( 1 + 6752 T + 45762873 T^{2} + 217324755008 T^{3} + 45762873 p^{7} T^{4} + 6752 p^{14} T^{5} + p^{21} T^{6} \) |
| 17 | $S_4\times C_2$ | \( 1 + 15418 T + 944657247 T^{2} + 9442063185964 T^{3} + 944657247 p^{7} T^{4} + 15418 p^{14} T^{5} + p^{21} T^{6} \) |
| 19 | $S_4\times C_2$ | \( 1 + 1826 T + 1600028897 T^{2} + 2952880404908 T^{3} + 1600028897 p^{7} T^{4} + 1826 p^{14} T^{5} + p^{21} T^{6} \) |
| 23 | $S_4\times C_2$ | \( 1 + 16536 T + 5773046325 T^{2} + 199623214893648 T^{3} + 5773046325 p^{7} T^{4} + 16536 p^{14} T^{5} + p^{21} T^{6} \) |
| 29 | $S_4\times C_2$ | \( 1 + 151194 T + 45098027259 T^{2} + 3976617395527644 T^{3} + 45098027259 p^{7} T^{4} + 151194 p^{14} T^{5} + p^{21} T^{6} \) |
| 31 | $S_4\times C_2$ | \( 1 + 46338 T + 72974004189 T^{2} + 2033145818541596 T^{3} + 72974004189 p^{7} T^{4} + 46338 p^{14} T^{5} + p^{21} T^{6} \) |
| 37 | $S_4\times C_2$ | \( 1 + 112378 T + 192745438499 T^{2} + 674114833374412 p T^{3} + 192745438499 p^{7} T^{4} + 112378 p^{14} T^{5} + p^{21} T^{6} \) |
| 41 | $S_4\times C_2$ | \( 1 - 324944 T + 411459972087 T^{2} - 80212219631459648 T^{3} + 411459972087 p^{7} T^{4} - 324944 p^{14} T^{5} + p^{21} T^{6} \) |
| 43 | $S_4\times C_2$ | \( 1 + 1282940 T + 733780085849 T^{2} + 315266904015983144 T^{3} + 733780085849 p^{7} T^{4} + 1282940 p^{14} T^{5} + p^{21} T^{6} \) |
| 47 | $S_4\times C_2$ | \( 1 + 917072 T + 137205467229 T^{2} - 350118715790347168 T^{3} + 137205467229 p^{7} T^{4} + 917072 p^{14} T^{5} + p^{21} T^{6} \) |
| 53 | $S_4\times C_2$ | \( 1 - 2688314 T + 5043235971075 T^{2} - 6031543406070306716 T^{3} + 5043235971075 p^{7} T^{4} - 2688314 p^{14} T^{5} + p^{21} T^{6} \) |
| 59 | $S_4\times C_2$ | \( 1 + 3176620 T + 7629317949849 T^{2} + 14621126030145146248 T^{3} + 7629317949849 p^{7} T^{4} + 3176620 p^{14} T^{5} + p^{21} T^{6} \) |
| 61 | $S_4\times C_2$ | \( 1 - 2165222 T + 10980954069371 T^{2} - 13978401435133476068 T^{3} + 10980954069371 p^{7} T^{4} - 2165222 p^{14} T^{5} + p^{21} T^{6} \) |
| 67 | $S_4\times C_2$ | \( 1 + 6699990 T + 32369890254177 T^{2} + 90880502558965082084 T^{3} + 32369890254177 p^{7} T^{4} + 6699990 p^{14} T^{5} + p^{21} T^{6} \) |
| 71 | $S_4\times C_2$ | \( 1 + 7734556 T + 576867347955 p T^{2} + \)\(14\!\cdots\!40\)\( T^{3} + 576867347955 p^{8} T^{4} + 7734556 p^{14} T^{5} + p^{21} T^{6} \) |
| 73 | $S_4\times C_2$ | \( 1 - 5784690 T + 28182816741639 T^{2} - \)\(11\!\cdots\!76\)\( T^{3} + 28182816741639 p^{7} T^{4} - 5784690 p^{14} T^{5} + p^{21} T^{6} \) |
| 79 | $S_4\times C_2$ | \( 1 + 8426640 T + 41929315141197 T^{2} + \)\(14\!\cdots\!20\)\( T^{3} + 41929315141197 p^{7} T^{4} + 8426640 p^{14} T^{5} + p^{21} T^{6} \) |
| 83 | $S_4\times C_2$ | \( 1 + 4126284 T + 69375413156721 T^{2} + \)\(18\!\cdots\!16\)\( T^{3} + 69375413156721 p^{7} T^{4} + 4126284 p^{14} T^{5} + p^{21} T^{6} \) |
| 89 | $S_4\times C_2$ | \( 1 - 5207756 T + 49568606983287 T^{2} + 31551267502524239704 T^{3} + 49568606983287 p^{7} T^{4} - 5207756 p^{14} T^{5} + p^{21} T^{6} \) |
| 97 | $S_4\times C_2$ | \( 1 + 7634614 T + 257400817130591 T^{2} + \)\(12\!\cdots\!96\)\( T^{3} + 257400817130591 p^{7} T^{4} + 7634614 p^{14} T^{5} + p^{21} T^{6} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{6} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.872526987742507218341422510334, −8.466752194946901413907098836893, −8.235359767317426838586837118282, −8.115805761695399990811642312569, −7.47280986893704083468909838085, −7.31586763608522084307329022418, −7.27248817908155464101431032533, −6.42732703459150763240088392172, −6.36591909420414740207917773753, −6.32414608909992670668019990730, −5.62707746856055699301879676294, −5.46183421476580201716979468877, −5.30955698198005598892554440107, −4.73088698000920394767860934032, −4.24921709743925783053465169778, −4.15711144788880462207941296799, −3.55712913923114882090570606172, −3.18274485695081728078502475567, −3.12668126873610415710908082829, −2.63067162149372059978779286243, −2.29027275128863803717365214718, −2.02997838936388062326449449968, −1.77208512796921478848548349805, −1.33046297881658333361406265164, −1.19478056140751261157470664560, 0, 0, 0,
1.19478056140751261157470664560, 1.33046297881658333361406265164, 1.77208512796921478848548349805, 2.02997838936388062326449449968, 2.29027275128863803717365214718, 2.63067162149372059978779286243, 3.12668126873610415710908082829, 3.18274485695081728078502475567, 3.55712913923114882090570606172, 4.15711144788880462207941296799, 4.24921709743925783053465169778, 4.73088698000920394767860934032, 5.30955698198005598892554440107, 5.46183421476580201716979468877, 5.62707746856055699301879676294, 6.32414608909992670668019990730, 6.36591909420414740207917773753, 6.42732703459150763240088392172, 7.27248817908155464101431032533, 7.31586763608522084307329022418, 7.47280986893704083468909838085, 8.115805761695399990811642312569, 8.235359767317426838586837118282, 8.466752194946901413907098836893, 8.872526987742507218341422510334