| L(s) = 1 | − 4·2-s + 12·4-s − 24·7-s − 32·8-s − 20·9-s + 52·11-s − 44·13-s + 96·14-s + 80·16-s − 100·17-s + 80·18-s + 38·19-s − 208·22-s − 16·23-s + 176·26-s − 288·28-s − 12·29-s − 16·31-s − 192·32-s + 400·34-s − 240·36-s − 36·37-s − 152·38-s + 148·41-s + 472·43-s + 624·44-s + 64·46-s + ⋯ |
| L(s) = 1 | − 1.41·2-s + 3/2·4-s − 1.29·7-s − 1.41·8-s − 0.740·9-s + 1.42·11-s − 0.938·13-s + 1.83·14-s + 5/4·16-s − 1.42·17-s + 1.04·18-s + 0.458·19-s − 2.01·22-s − 0.145·23-s + 1.32·26-s − 1.94·28-s − 0.0768·29-s − 0.0926·31-s − 1.06·32-s + 2.01·34-s − 1.11·36-s − 0.159·37-s − 0.648·38-s + 0.563·41-s + 1.67·43-s + 2.13·44-s + 0.205·46-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 902500 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 902500 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(2)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_1$ | \( ( 1 + p T )^{2} \) |
| 5 | | \( 1 \) |
| 19 | $C_1$ | \( ( 1 - p T )^{2} \) |
| good | 3 | $C_2^2$ | \( 1 + 20 T^{2} + p^{6} T^{4} \) |
| 7 | $D_{4}$ | \( 1 + 24 T + 694 T^{2} + 24 p^{3} T^{3} + p^{6} T^{4} \) |
| 11 | $D_{4}$ | \( 1 - 52 T + 3202 T^{2} - 52 p^{3} T^{3} + p^{6} T^{4} \) |
| 13 | $D_{4}$ | \( 1 + 44 T + 4028 T^{2} + 44 p^{3} T^{3} + p^{6} T^{4} \) |
| 17 | $D_{4}$ | \( 1 + 100 T + 12190 T^{2} + 100 p^{3} T^{3} + p^{6} T^{4} \) |
| 23 | $D_{4}$ | \( 1 + 16 T + 22222 T^{2} + 16 p^{3} T^{3} + p^{6} T^{4} \) |
| 29 | $D_{4}$ | \( 1 + 12 T + 37798 T^{2} + 12 p^{3} T^{3} + p^{6} T^{4} \) |
| 31 | $D_{4}$ | \( 1 + 16 T + 46046 T^{2} + 16 p^{3} T^{3} + p^{6} T^{4} \) |
| 37 | $D_{4}$ | \( 1 + 36 T + 68956 T^{2} + 36 p^{3} T^{3} + p^{6} T^{4} \) |
| 41 | $D_{4}$ | \( 1 - 148 T + 120334 T^{2} - 148 p^{3} T^{3} + p^{6} T^{4} \) |
| 43 | $D_{4}$ | \( 1 - 472 T + 191726 T^{2} - 472 p^{3} T^{3} + p^{6} T^{4} \) |
| 47 | $D_{4}$ | \( 1 + 8 p T + 220006 T^{2} + 8 p^{4} T^{3} + p^{6} T^{4} \) |
| 53 | $D_{4}$ | \( 1 + 116 T + 226012 T^{2} + 116 p^{3} T^{3} + p^{6} T^{4} \) |
| 59 | $D_{4}$ | \( 1 - 112 T + 185278 T^{2} - 112 p^{3} T^{3} + p^{6} T^{4} \) |
| 61 | $D_{4}$ | \( 1 + 680 T + 525498 T^{2} + 680 p^{3} T^{3} + p^{6} T^{4} \) |
| 67 | $D_{4}$ | \( 1 - 208 T + 305492 T^{2} - 208 p^{3} T^{3} + p^{6} T^{4} \) |
| 71 | $D_{4}$ | \( 1 + 616 T + 797086 T^{2} + 616 p^{3} T^{3} + p^{6} T^{4} \) |
| 73 | $D_{4}$ | \( 1 - 1332 T + 1214926 T^{2} - 1332 p^{3} T^{3} + p^{6} T^{4} \) |
| 79 | $D_{4}$ | \( 1 - 216 T + 697318 T^{2} - 216 p^{3} T^{3} + p^{6} T^{4} \) |
| 83 | $D_{4}$ | \( 1 - 40 T - 7130 T^{2} - 40 p^{3} T^{3} + p^{6} T^{4} \) |
| 89 | $D_{4}$ | \( 1 - 484 T + 1445518 T^{2} - 484 p^{3} T^{3} + p^{6} T^{4} \) |
| 97 | $D_{4}$ | \( 1 + 556 T + 1850916 T^{2} + 556 p^{3} T^{3} + p^{6} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
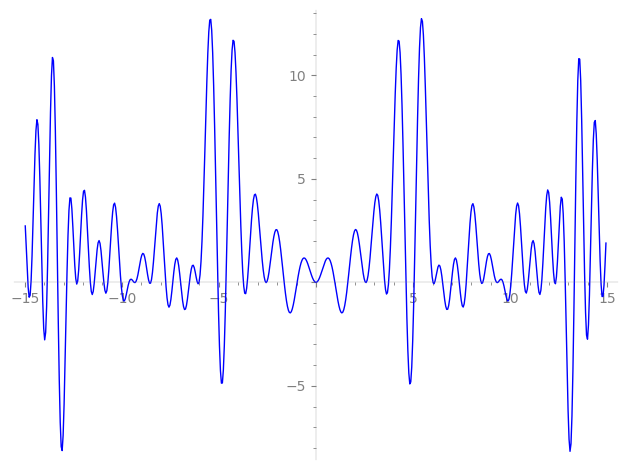
Imaginary part of the first few zeros on the critical line
−9.365299711366084124751022872133, −9.300955812763725292800805014342, −8.588463974427202792646294386502, −8.503022440738057518317411209871, −7.73704984951609419730351711716, −7.37611454193625767078687385951, −6.97339781165463479743315620092, −6.51898807609288309969010266628, −6.11043860896905627192563291448, −6.02467687218854377713839072561, −5.05514085975292393667364986576, −4.63437187075312310753632682078, −3.73776599407676503871005372528, −3.53920774176807849611728869872, −2.58887683961576895271617582891, −2.54617760787408810039457998227, −1.63901535147391791975134933466, −0.971540451772281909162407545151, 0, 0,
0.971540451772281909162407545151, 1.63901535147391791975134933466, 2.54617760787408810039457998227, 2.58887683961576895271617582891, 3.53920774176807849611728869872, 3.73776599407676503871005372528, 4.63437187075312310753632682078, 5.05514085975292393667364986576, 6.02467687218854377713839072561, 6.11043860896905627192563291448, 6.51898807609288309969010266628, 6.97339781165463479743315620092, 7.37611454193625767078687385951, 7.73704984951609419730351711716, 8.503022440738057518317411209871, 8.588463974427202792646294386502, 9.300955812763725292800805014342, 9.365299711366084124751022872133