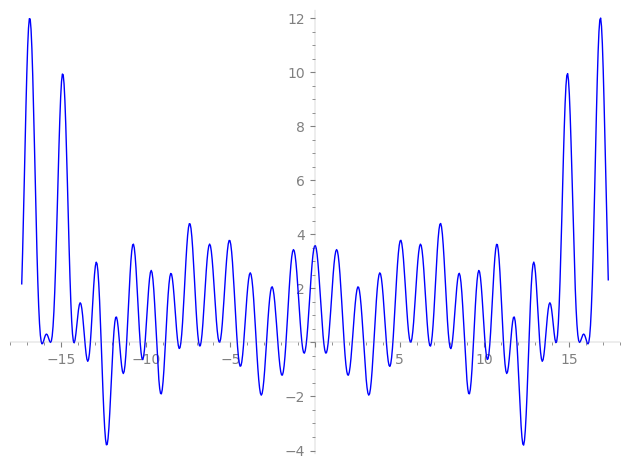
| L(s) = 1 | + 5.36e4·5-s − 3.33e5·7-s − 4.30e8·11-s + 2.66e9·13-s − 6.06e10·17-s + 1.78e11·19-s − 5.28e11·23-s − 1.01e12·25-s + 7.24e12·29-s − 1.87e12·31-s − 1.78e10·35-s − 2.03e13·37-s + 1.76e12·41-s + 1.93e14·43-s − 1.00e14·47-s − 3.30e14·49-s + 3.17e14·53-s − 2.31e13·55-s + 1.26e15·59-s + 2.76e15·61-s + 1.43e14·65-s + 1.96e15·67-s − 4.83e14·71-s − 2.17e15·73-s + 1.43e14·77-s − 5.29e15·79-s − 9.97e15·83-s + ⋯ |
| L(s) = 1 | + 0.0613·5-s − 0.0218·7-s − 0.606·11-s + 0.906·13-s − 2.10·17-s + 2.41·19-s − 1.40·23-s − 1.33·25-s + 2.68·29-s − 0.395·31-s − 0.00134·35-s − 0.951·37-s + 0.0344·41-s + 2.52·43-s − 0.617·47-s − 1.42·49-s + 0.701·53-s − 0.0372·55-s + 1.11·59-s + 1.84·61-s + 0.0556·65-s + 0.590·67-s − 0.0888·71-s − 0.315·73-s + 0.0132·77-s − 0.392·79-s − 0.486·83-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 5184 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(18-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 5184 ^{s/2} \, \Gamma_{\C}(s+17/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(9)\) |
\(\approx\) |
\(3.597635467\) |
| \(L(\frac12)\) |
\(\approx\) |
\(3.597635467\) |
| \(L(\frac{19}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| good | 5 | $D_{4}$ | \( 1 - 10724 p T + 8162342086 p^{3} T^{2} - 10724 p^{18} T^{3} + p^{34} T^{4} \) |
| 7 | $D_{4}$ | \( 1 + 333168 T + 6750380073134 p^{2} T^{2} + 333168 p^{17} T^{3} + p^{34} T^{4} \) |
| 11 | $D_{4}$ | \( 1 + 430974680 T + 24621881623740466 p T^{2} + 430974680 p^{17} T^{3} + p^{34} T^{4} \) |
| 13 | $D_{4}$ | \( 1 - 205193996 p T + 22476549286509102 p^{2} T^{2} - 205193996 p^{18} T^{3} + p^{34} T^{4} \) |
| 17 | $D_{4}$ | \( 1 + 3569029604 p T + \)\(22\!\cdots\!74\)\( T^{2} + 3569029604 p^{18} T^{3} + p^{34} T^{4} \) |
| 19 | $D_{4}$ | \( 1 - 178629960040 T + \)\(18\!\cdots\!42\)\( T^{2} - 178629960040 p^{17} T^{3} + p^{34} T^{4} \) |
| 23 | $D_{4}$ | \( 1 + 528756594608 T + \)\(30\!\cdots\!38\)\( T^{2} + 528756594608 p^{17} T^{3} + p^{34} T^{4} \) |
| 29 | $D_{4}$ | \( 1 - 7240660091460 T + \)\(26\!\cdots\!54\)\( T^{2} - 7240660091460 p^{17} T^{3} + p^{34} T^{4} \) |
| 31 | $D_{4}$ | \( 1 + 1878351140288 T + \)\(42\!\cdots\!42\)\( T^{2} + 1878351140288 p^{17} T^{3} + p^{34} T^{4} \) |
| 37 | $D_{4}$ | \( 1 + 20332464566580 T + \)\(11\!\cdots\!98\)\( T^{2} + 20332464566580 p^{17} T^{3} + p^{34} T^{4} \) |
| 41 | $D_{4}$ | \( 1 - 1763041905324 T + \)\(20\!\cdots\!10\)\( T^{2} - 1763041905324 p^{17} T^{3} + p^{34} T^{4} \) |
| 43 | $D_{4}$ | \( 1 - 193394525968664 T + \)\(20\!\cdots\!54\)\( T^{2} - 193394525968664 p^{17} T^{3} + p^{34} T^{4} \) |
| 47 | $D_{4}$ | \( 1 + 100763837765472 T + \)\(33\!\cdots\!70\)\( T^{2} + 100763837765472 p^{17} T^{3} + p^{34} T^{4} \) |
| 53 | $D_{4}$ | \( 1 - 317818146060052 T + \)\(20\!\cdots\!02\)\( T^{2} - 317818146060052 p^{17} T^{3} + p^{34} T^{4} \) |
| 59 | $D_{4}$ | \( 1 - 1262050788321736 T + \)\(18\!\cdots\!06\)\( T^{2} - 1262050788321736 p^{17} T^{3} + p^{34} T^{4} \) |
| 61 | $D_{4}$ | \( 1 - 2765859692723708 T + \)\(50\!\cdots\!62\)\( T^{2} - 2765859692723708 p^{17} T^{3} + p^{34} T^{4} \) |
| 67 | $D_{4}$ | \( 1 - 1963006544550088 T + \)\(22\!\cdots\!46\)\( T^{2} - 1963006544550088 p^{17} T^{3} + p^{34} T^{4} \) |
| 71 | $D_{4}$ | \( 1 + 483639107104528 T + \)\(58\!\cdots\!42\)\( T^{2} + 483639107104528 p^{17} T^{3} + p^{34} T^{4} \) |
| 73 | $D_{4}$ | \( 1 + 2176892348591212 T + \)\(18\!\cdots\!58\)\( T^{2} + 2176892348591212 p^{17} T^{3} + p^{34} T^{4} \) |
| 79 | $D_{4}$ | \( 1 + 5295839905627744 T + \)\(33\!\cdots\!98\)\( T^{2} + 5295839905627744 p^{17} T^{3} + p^{34} T^{4} \) |
| 83 | $D_{4}$ | \( 1 + 9972518018887144 T + \)\(81\!\cdots\!34\)\( T^{2} + 9972518018887144 p^{17} T^{3} + p^{34} T^{4} \) |
| 89 | $D_{4}$ | \( 1 - 711099036813900 T + \)\(23\!\cdots\!82\)\( T^{2} - 711099036813900 p^{17} T^{3} + p^{34} T^{4} \) |
| 97 | $D_{4}$ | \( 1 - 114870546609971908 T + \)\(15\!\cdots\!90\)\( T^{2} - 114870546609971908 p^{17} T^{3} + p^{34} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−11.55242357403052132953392424995, −11.13181969800023139233647634810, −10.33122206881437212855221170589, −10.04174349842828385013274524412, −9.358034453997677015259672725875, −8.837317301513892883492749414125, −8.105685997019956138646514526606, −7.924774314194086063413582918913, −6.87462340981718803887085772078, −6.73442549426857155622679816265, −5.65119614920540439413714961241, −5.64344336874542201996364508970, −4.59726365927076352928859266210, −4.21448754240570988310744696410, −3.47369273023786899852732819474, −2.86856800628419632698596796236, −2.19755396567541405929158196599, −1.71775431994149114024069024839, −0.77677514653405817543101058383, −0.51162266774917535473090230807,
0.51162266774917535473090230807, 0.77677514653405817543101058383, 1.71775431994149114024069024839, 2.19755396567541405929158196599, 2.86856800628419632698596796236, 3.47369273023786899852732819474, 4.21448754240570988310744696410, 4.59726365927076352928859266210, 5.64344336874542201996364508970, 5.65119614920540439413714961241, 6.73442549426857155622679816265, 6.87462340981718803887085772078, 7.924774314194086063413582918913, 8.105685997019956138646514526606, 8.837317301513892883492749414125, 9.358034453997677015259672725875, 10.04174349842828385013274524412, 10.33122206881437212855221170589, 11.13181969800023139233647634810, 11.55242357403052132953392424995