↑

Properties

Label 4-3520e2-1.1-c0e2-0-0
Degree $4$
Conductor $12390400$
Sign $1$
Analytic cond. $3.08602$
Root an. cond. $1.32540$
Motivic weight $0$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

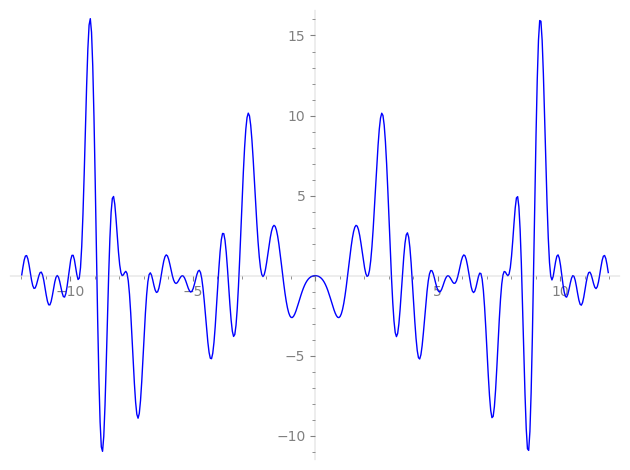
L(s)  = 1  − 2·3-s + 2·9-s − 2·11-s − 2·23-s − 25-s − 2·27-s + 4·33-s − 2·37-s − 2·47-s − 2·53-s + 2·67-s + 4·69-s + 2·75-s + 3·81-s + 2·97-s − 4·99-s − 2·103-s + 4·111-s − 2·113-s + 3·121-s + 127-s + 131-s + 137-s + 139-s + 4·141-s + 149-s + 151-s + ⋯
L(s)  = 1  − 2·3-s + 2·9-s − 2·11-s − 2·23-s − 25-s − 2·27-s + 4·33-s − 2·37-s − 2·47-s − 2·53-s + 2·67-s + 4·69-s + 2·75-s + 3·81-s + 2·97-s − 4·99-s − 2·103-s + 4·111-s − 2·113-s + 3·121-s + 127-s + 131-s + 137-s + 139-s + 4·141-s + 149-s + 151-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 12390400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 12390400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(12390400\)    =    \(2^{12} \cdot 5^{2} \cdot 11^{2}\)
Sign: $1$
Analytic conductor: \(3.08602\)
Root analytic conductor: \(1.32540\)
Motivic weight: \(0\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 12390400,\ (\ :0, 0),\ 1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.003239846520\)
\(L(\frac12)\) \(\approx\) \(0.003239846520\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad2 \( 1 \)
5$C_2$ \( 1 + T^{2} \)
11$C_1$ \( ( 1 + T )^{2} \)
good3$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
7$C_2^2$ \( 1 + T^{4} \)
13$C_2^2$ \( 1 + T^{4} \)
17$C_2^2$ \( 1 + T^{4} \)
19$C_2$ \( ( 1 + T^{2} )^{2} \)
23$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
29$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
31$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
37$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
41$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
43$C_2^2$ \( 1 + T^{4} \)
47$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
53$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
59$C_2$ \( ( 1 + T^{2} )^{2} \)
61$C_2$ \( ( 1 + T^{2} )^{2} \)
67$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
71$C_2$ \( ( 1 + T^{2} )^{2} \)
73$C_2^2$ \( 1 + T^{4} \)
79$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
83$C_2^2$ \( 1 + T^{4} \)
89$C_2$ \( ( 1 + T^{2} )^{2} \)
97$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−9.724639428709969867274883423968, −8.433337785352409371040172300179, −7.88043825593981561041928878682, −7.86102514597649175134468898760, −7.66226964472359892825110426837, −6.79283427612589252416153071894, −6.67579646683117667629956986929, −6.28796589333581658989611446064, −5.83140011224273046319223952057, −5.42919415248754779901402645284, −5.41513518314100471329200752756, −4.84413886280981823855514906996, −4.65149972701137485367859212997, −3.95201260587453819523916837872, −3.56149051327744326820139602861, −3.11251612258262522295302806723, −2.16478575205042957306685838225, −2.09739748128686546885456651641, −1.32392995520760292387923656621, −0.03779647940376926955555201538, 0.03779647940376926955555201538, 1.32392995520760292387923656621, 2.09739748128686546885456651641, 2.16478575205042957306685838225, 3.11251612258262522295302806723, 3.56149051327744326820139602861, 3.95201260587453819523916837872, 4.65149972701137485367859212997, 4.84413886280981823855514906996, 5.41513518314100471329200752756, 5.42919415248754779901402645284, 5.83140011224273046319223952057, 6.28796589333581658989611446064, 6.67579646683117667629956986929, 6.79283427612589252416153071894, 7.66226964472359892825110426837, 7.86102514597649175134468898760, 7.88043825593981561041928878682, 8.433337785352409371040172300179, 9.724639428709969867274883423968

Graph of the $Z$-function along the critical line