| L(s) = 1 | + 16·2-s − 42·3-s + 192·4-s + 550·5-s − 672·6-s + 2.04e3·8-s + 882·9-s + 8.80e3·10-s + 1.78e3·11-s − 8.06e3·12-s − 3.04e3·13-s − 2.31e4·15-s + 2.04e4·16-s + 4.52e4·17-s + 1.41e4·18-s − 2.41e4·19-s + 1.05e5·20-s + 2.85e4·22-s + 5.32e4·23-s − 8.60e4·24-s + 2.24e5·25-s − 4.86e4·26-s − 9.18e4·27-s − 3.69e5·30-s + 1.48e5·31-s + 1.96e5·32-s − 7.50e4·33-s + ⋯ |
| L(s) = 1 | + 1.41·2-s − 0.898·3-s + 3/2·4-s + 1.96·5-s − 1.27·6-s + 1.41·8-s + 0.403·9-s + 2.78·10-s + 0.404·11-s − 1.34·12-s − 0.384·13-s − 1.76·15-s + 5/4·16-s + 2.23·17-s + 0.570·18-s − 0.806·19-s + 2.95·20-s + 0.572·22-s + 0.912·23-s − 1.27·24-s + 2.87·25-s − 0.543·26-s − 0.898·27-s − 2.49·30-s + 0.896·31-s + 1.06·32-s − 0.363·33-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 16900 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(8-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 16900 ^{s/2} \, \Gamma_{\C}(s+7/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(4)\) |
\(\approx\) |
\(11.94462523\) |
| \(L(\frac12)\) |
\(\approx\) |
\(11.94462523\) |
| \(L(\frac{9}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_1$ | \( ( 1 - p^{3} T )^{2} \) |
| 5 | $C_2$ | \( 1 - 22 p^{2} T + p^{7} T^{2} \) |
| 13 | $C_2$ | \( 1 + 18 p^{2} T + p^{7} T^{2} \) |
| good | 3 | $C_2^2$ | \( 1 + 14 p T + 98 p^{2} T^{2} + 14 p^{8} T^{3} + p^{14} T^{4} \) |
| 7 | $C_2^2$ | \( 1 - 1488682 T^{2} + p^{14} T^{4} \) |
| 11 | $C_2^2$ | \( 1 - 1786 T + 1594898 T^{2} - 1786 p^{7} T^{3} + p^{14} T^{4} \) |
| 17 | $C_2^2$ | \( 1 - 45218 T + 1022333762 T^{2} - 45218 p^{7} T^{3} + p^{14} T^{4} \) |
| 19 | $C_2^2$ | \( 1 + 24126 T + 291031938 T^{2} + 24126 p^{7} T^{3} + p^{14} T^{4} \) |
| 23 | $C_2^2$ | \( 1 - 53218 T + 1416077762 T^{2} - 53218 p^{7} T^{3} + p^{14} T^{4} \) |
| 29 | $C_2^2$ | \( 1 - 21038184042 T^{2} + p^{14} T^{4} \) |
| 31 | $C_2^2$ | \( 1 - 148718 T + 11058521762 T^{2} - 148718 p^{7} T^{3} + p^{14} T^{4} \) |
| 37 | $C_2^2$ | \( 1 - 9687275482 T^{2} + p^{14} T^{4} \) |
| 41 | $C_2^2$ | \( 1 + 310622 T + 48243013442 T^{2} + 310622 p^{7} T^{3} + p^{14} T^{4} \) |
| 43 | $C_2^2$ | \( 1 - 1372282 T + 941578943762 T^{2} - 1372282 p^{7} T^{3} + p^{14} T^{4} \) |
| 47 | $C_2^2$ | \( 1 - 27193268922 T^{2} + p^{14} T^{4} \) |
| 53 | $C_2^2$ | \( 1 - 1997834 T + 1995670345778 T^{2} - 1997834 p^{7} T^{3} + p^{14} T^{4} \) |
| 59 | $C_2^2$ | \( 1 + 3317226 T + 5501994167538 T^{2} + 3317226 p^{7} T^{3} + p^{14} T^{4} \) |
| 61 | $C_2$ | \( ( 1 - 1418858 T + p^{7} T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 + 2306772 T + p^{7} T^{2} )^{2} \) |
| 71 | $C_2^2$ | \( 1 - 7300726 T + 26650300063538 T^{2} - 7300726 p^{7} T^{3} + p^{14} T^{4} \) |
| 73 | $C_2$ | \( ( 1 + 1200810 T + p^{7} T^{2} )^{2} \) |
| 79 | $C_2^2$ | \( 1 - 5989211109562 T^{2} + p^{14} T^{4} \) |
| 83 | $C_2^2$ | \( 1 - 53589287320978 T^{2} + p^{14} T^{4} \) |
| 89 | $C_2^2$ | \( 1 - 1784570 T + 1592345042450 T^{2} - 1784570 p^{7} T^{3} + p^{14} T^{4} \) |
| 97 | $C_2$ | \( ( 1 + 8971790 T + p^{7} T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
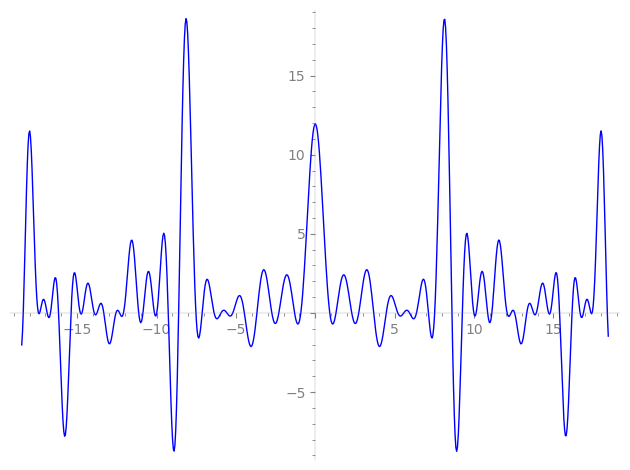
Imaginary part of the first few zeros on the critical line
−12.32888596854133035750639626986, −12.08444000202650831415880130827, −11.12317219842320198372180458373, −10.85806517411638838574311881743, −10.13233061335225539081349189579, −9.987764352638468971463681139498, −9.261722553612931123127073159448, −8.608134439168671803350192275133, −7.51908116471849176828392736320, −7.12852515917071430229785867384, −6.37450485554142525338239655275, −5.94099702509916530345348666597, −5.57020916966354309732054671375, −5.19893215944588972751949244216, −4.46880782229784267236298092978, −3.67835353274466869604127477674, −2.73666244188188623594697574570, −2.29766963589183433892943482977, −1.30370734922500465906115500478, −0.913110398182849396810636458874,
0.913110398182849396810636458874, 1.30370734922500465906115500478, 2.29766963589183433892943482977, 2.73666244188188623594697574570, 3.67835353274466869604127477674, 4.46880782229784267236298092978, 5.19893215944588972751949244216, 5.57020916966354309732054671375, 5.94099702509916530345348666597, 6.37450485554142525338239655275, 7.12852515917071430229785867384, 7.51908116471849176828392736320, 8.608134439168671803350192275133, 9.261722553612931123127073159448, 9.987764352638468971463681139498, 10.13233061335225539081349189579, 10.85806517411638838574311881743, 11.12317219842320198372180458373, 12.08444000202650831415880130827, 12.32888596854133035750639626986