↑

Properties

Label 2-87-87.86-c4-0-24
Degree $2$
Conductor $87$
Sign $0.395 - 0.918i$
Analytic cond. $8.99318$
Root an. cond. $2.99886$
Motivic weight $4$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

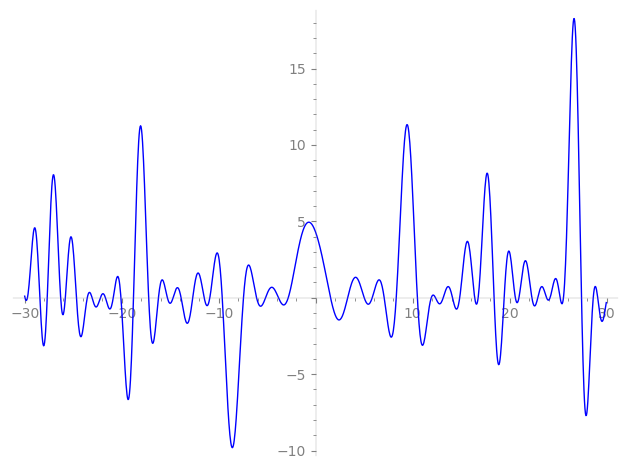
L(s)  = 1  + 7.23·2-s + (−2.40 + 8.67i)3-s + 36.3·4-s + 19.6i·5-s + (−17.4 + 62.7i)6-s − 0.405·7-s + 147.·8-s + (−69.3 − 41.7i)9-s + 141. i·10-s − 13.1·11-s + (−87.5 + 315. i)12-s + 2.15·13-s − 2.93·14-s + (−170. − 47.2i)15-s + 484.·16-s + 467.·17-s + ⋯
L(s)  = 1  + 1.80·2-s + (−0.267 + 0.963i)3-s + 2.27·4-s + 0.784i·5-s + (−0.484 + 1.74i)6-s − 0.00827·7-s + 2.30·8-s + (−0.856 − 0.515i)9-s + 1.41i·10-s − 0.108·11-s + (−0.608 + 2.18i)12-s + 0.0127·13-s − 0.0149·14-s + (−0.756 − 0.210i)15-s + 1.89·16-s + 1.61·17-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 87 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.395 - 0.918i)\, \overline{\Lambda}(5-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 87 ^{s/2} \, \Gamma_{\C}(s+2) \, L(s)\cr =\mathstrut & (0.395 - 0.918i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(87\)    =    \(3 \cdot 29\)
Sign: $0.395 - 0.918i$
Analytic conductor: \(8.99318\)
Root analytic conductor: \(2.99886\)
Motivic weight: \(4\)
Rational: no
Arithmetic: yes
Character: $\chi_{87} (86, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 87,\ (\ :2),\ 0.395 - 0.918i)\)

Particular Values

\(L(\frac{5}{2})\) \(\approx\) \(3.56855 + 2.34806i\)
\(L(\frac12)\) \(\approx\) \(3.56855 + 2.34806i\)
\(L(3)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 + (2.40 - 8.67i)T \)
29 \( 1 + (833. + 113. i)T \)
good2 \( 1 - 7.23T + 16T^{2} \)
5 \( 1 - 19.6iT - 625T^{2} \)
7 \( 1 + 0.405T + 2.40e3T^{2} \)
11 \( 1 + 13.1T + 1.46e4T^{2} \)
13 \( 1 - 2.15T + 2.85e4T^{2} \)
17 \( 1 - 467.T + 8.35e4T^{2} \)
19 \( 1 + 421. iT - 1.30e5T^{2} \)
23 \( 1 - 399. iT - 2.79e5T^{2} \)
31 \( 1 + 1.44e3iT - 9.23e5T^{2} \)
37 \( 1 + 1.63e3iT - 1.87e6T^{2} \)
41 \( 1 + 1.27e3T + 2.82e6T^{2} \)
43 \( 1 - 1.80e3iT - 3.41e6T^{2} \)
47 \( 1 - 1.52e3T + 4.87e6T^{2} \)
53 \( 1 - 4.75e3iT - 7.89e6T^{2} \)
59 \( 1 + 2.41e3iT - 1.21e7T^{2} \)
61 \( 1 + 5.16e3iT - 1.38e7T^{2} \)
67 \( 1 + 1.68e3T + 2.01e7T^{2} \)
71 \( 1 - 3.64e3iT - 2.54e7T^{2} \)
73 \( 1 - 8.32e3iT - 2.83e7T^{2} \)
79 \( 1 + 5.80e3iT - 3.89e7T^{2} \)
83 \( 1 - 2.30e3iT - 4.74e7T^{2} \)
89 \( 1 + 4.00e3T + 6.27e7T^{2} \)
97 \( 1 - 1.10e4iT - 8.85e7T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−13.87833033714433639124729738828, −12.67767908506690919265928488033, −11.49827713509210672810045036474, −10.91733526749499858373061228824, −9.637291530276070437914952988848, −7.44687097364035508498267972479, −6.09903132434988102352346688627, −5.17141196958317920990597731423, −3.84147508784275338012755921354, −2.83394556782490276307912661294, 1.52823223802981937850232484611, 3.29227387641621799347520211689, 4.99870911577198371201458620193, 5.82368493791214917543851609864, 7.05669565938927203420586613344, 8.299905249502464395344597150951, 10.47826262303706115223290025833, 11.91146958533640311649841720115, 12.34470915300548213736431783043, 13.14096964837317396012582205980

Graph of the $Z$-function along the critical line