↑

Properties

Label 2-768-24.11-c1-0-3
Degree 22
Conductor 768768
Sign 0.408−0.912i0.408 - 0.912i
Analytic cond. 6.132516.13251
Root an. cond. 2.476392.47639
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.61 + 0.618i)3-s − 3.23·5-s − 1.23i·7-s + (2.23 − 2.00i)9-s − 5.23i·11-s + 4.47i·13-s + (5.23 − 2.00i)15-s + 2.47i·17-s + 0.763·19-s + (0.763 + 2.00i)21-s − 2.47·23-s + 5.47·25-s + (−2.38 + 4.61i)27-s + 4.76·29-s + 5.23i·31-s + ⋯
L(s)  = 1  + (−0.934 + 0.356i)3-s − 1.44·5-s − 0.467i·7-s + (0.745 − 0.666i)9-s − 1.57i·11-s + 1.24i·13-s + (1.35 − 0.516i)15-s + 0.599i·17-s + 0.175·19-s + (0.166 + 0.436i)21-s − 0.515·23-s + 1.09·25-s + (−0.458 + 0.888i)27-s + 0.884·29-s + 0.940i·31-s + ⋯

Functional equation

Λ(s)=(768s/2 ΓC(s) L(s)=((0.408−0.912i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 768 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.408 - 0.912i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(768s/2 ΓC(s+1/2) L(s)=((0.408−0.912i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 768 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.408 - 0.912i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 768768    =    28⋅32^{8} \cdot 3
Sign: 0.408−0.912i0.408 - 0.912i
Analytic conductor: 6.132516.13251
Root analytic conductor: 2.476392.47639
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ768(383,⋅)\chi_{768} (383, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 768, ( :1/2), 0.408−0.912i)(2,\ 768,\ (\ :1/2),\ 0.408 - 0.912i)

Particular Values

L(1)L(1) ≈\approx 0.524616+0.340072i0.524616 + 0.340072i
L(12)L(\frac12) ≈\approx 0.524616+0.340072i0.524616 + 0.340072i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
3 1+(1.61−0.618i)T 1 + (1.61 - 0.618i)T
good5 1+3.23T+5T2 1 + 3.23T + 5T^{2}
7 1+1.23iT−7T2 1 + 1.23iT - 7T^{2}
11 1+5.23iT−11T2 1 + 5.23iT - 11T^{2}
13 1−4.47iT−13T2 1 - 4.47iT - 13T^{2}
17 1−2.47iT−17T2 1 - 2.47iT - 17T^{2}
19 1−0.763T+19T2 1 - 0.763T + 19T^{2}
23 1+2.47T+23T2 1 + 2.47T + 23T^{2}
29 1−4.76T+29T2 1 - 4.76T + 29T^{2}
31 1−5.23iT−31T2 1 - 5.23iT - 31T^{2}
37 1−8.47iT−37T2 1 - 8.47iT - 37T^{2}
41 1−6.47iT−41T2 1 - 6.47iT - 41T^{2}
43 1−7.23T+43T2 1 - 7.23T + 43T^{2}
47 1+8T+47T2 1 + 8T + 47T^{2}
53 1+3.23T+53T2 1 + 3.23T + 53T^{2}
59 1−1.23iT−59T2 1 - 1.23iT - 59T^{2}
61 1+0.472iT−61T2 1 + 0.472iT - 61T^{2}
67 1−9.70T+67T2 1 - 9.70T + 67T^{2}
71 1−15.4T+71T2 1 - 15.4T + 71T^{2}
73 1−2T+73T2 1 - 2T + 73T^{2}
79 1−0.291iT−79T2 1 - 0.291iT - 79T^{2}
83 1−2.76iT−83T2 1 - 2.76iT - 83T^{2}
89 1−4iT−89T2 1 - 4iT - 89T^{2}
97 1−0.472T+97T2 1 - 0.472T + 97T^{2}
show more
show less
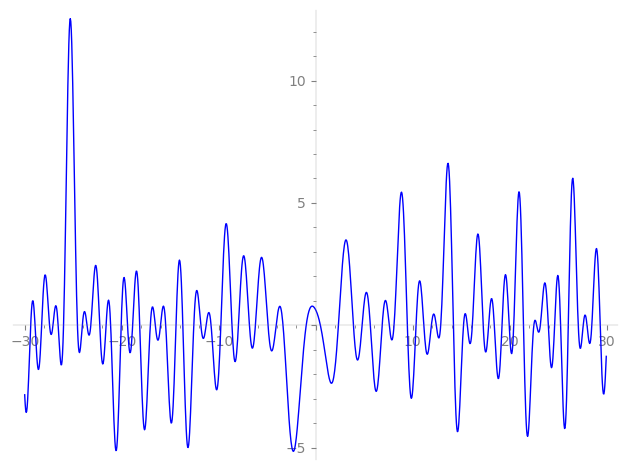
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.78676894994886900847162676249, −9.780792051735879161479432725278, −8.633394749435101373939546296598, −7.966907365744911266720988421156, −6.83332850925299462284188648999, −6.21752813489160752839231896883, −4.91999316105519288251409516356, −4.07998570040077863170079467191, −3.37140658726089546864194931169, −0.981546609604123035453254277812, 0.47925865927692612212045167709, 2.33752077307676352294556198400, 3.88490084153041906223180962243, 4.78066862679563805895927793679, 5.62772530751221583752710294768, 6.84775663259973337774910849398, 7.57992738761191657202383396808, 8.073063598712233606110549096723, 9.442998909953476232287960401230, 10.33945484151978311406494592771

Graph of the ZZ-function along the critical line