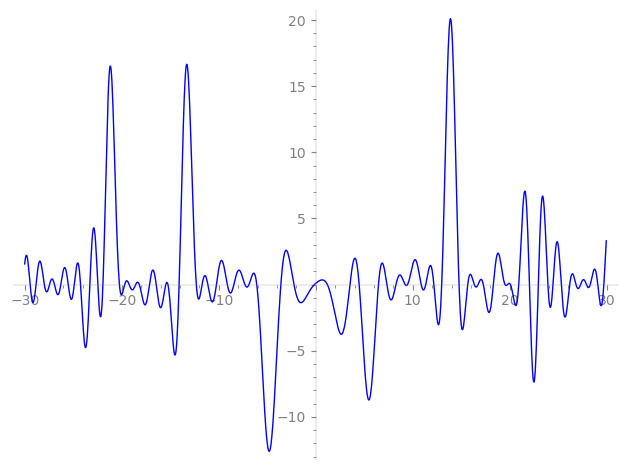
| L(s) = 1 | + (−2.58 + 0.339i)2-s + (−0.442 − 0.896i)3-s + (4.61 − 1.23i)4-s + (−3.08 + 2.70i)5-s + (1.44 + 2.16i)6-s + (−1.79 + 1.94i)7-s + (−6.69 + 2.77i)8-s + (−0.608 + 0.793i)9-s + (7.04 − 8.03i)10-s + (4.54 − 0.297i)11-s + (−3.15 − 3.59i)12-s + (−0.442 − 0.442i)13-s + (3.97 − 5.63i)14-s + (3.79 + 1.57i)15-s + (8.06 − 4.65i)16-s + (−3.90 − 1.32i)17-s + ⋯ |
| L(s) = 1 | + (−1.82 + 0.240i)2-s + (−0.255 − 0.517i)3-s + (2.30 − 0.618i)4-s + (−1.38 + 1.21i)5-s + (0.590 + 0.884i)6-s + (−0.678 + 0.735i)7-s + (−2.36 + 0.980i)8-s + (−0.202 + 0.264i)9-s + (2.22 − 2.54i)10-s + (1.37 − 0.0898i)11-s + (−0.910 − 1.03i)12-s + (−0.122 − 0.122i)13-s + (1.06 − 1.50i)14-s + (0.979 + 0.405i)15-s + (2.01 − 1.16i)16-s + (−0.946 − 0.321i)17-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 357 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.329 + 0.944i)\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 357 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.329 + 0.944i)\, \overline{\Lambda}(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.0536651 - 0.0755340i\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.0536651 - 0.0755340i\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 3 | \( 1 + (0.442 + 0.896i)T \) |
| 7 | \( 1 + (1.79 - 1.94i)T \) |
| 17 | \( 1 + (3.90 + 1.32i)T \) |
| good | 2 | \( 1 + (2.58 - 0.339i)T + (1.93 - 0.517i)T^{2} \) |
| 5 | \( 1 + (3.08 - 2.70i)T + (0.652 - 4.95i)T^{2} \) |
| 11 | \( 1 + (-4.54 + 0.297i)T + (10.9 - 1.43i)T^{2} \) |
| 13 | \( 1 + (0.442 + 0.442i)T + 13iT^{2} \) |
| 19 | \( 1 + (-0.178 - 1.35i)T + (-18.3 + 4.91i)T^{2} \) |
| 23 | \( 1 + (0.0864 + 0.0426i)T + (14.0 + 18.2i)T^{2} \) |
| 29 | \( 1 + (0.976 + 4.90i)T + (-26.7 + 11.0i)T^{2} \) |
| 31 | \( 1 + (6.44 - 3.17i)T + (18.8 - 24.5i)T^{2} \) |
| 37 | \( 1 + (0.0907 - 1.38i)T + (-36.6 - 4.82i)T^{2} \) |
| 41 | \( 1 + (-1.16 + 5.85i)T + (-37.8 - 15.6i)T^{2} \) |
| 43 | \( 1 + (4.24 + 10.2i)T + (-30.4 + 30.4i)T^{2} \) |
| 47 | \( 1 + (-1.65 + 6.16i)T + (-40.7 - 23.5i)T^{2} \) |
| 53 | \( 1 + (-3.05 - 3.98i)T + (-13.7 + 51.1i)T^{2} \) |
| 59 | \( 1 + (8.45 + 1.11i)T + (56.9 + 15.2i)T^{2} \) |
| 61 | \( 1 + (0.0779 + 0.229i)T + (-48.3 + 37.1i)T^{2} \) |
| 67 | \( 1 + (1.28 + 0.742i)T + (33.5 + 58.0i)T^{2} \) |
| 71 | \( 1 + (-2.41 - 1.61i)T + (27.1 + 65.5i)T^{2} \) |
| 73 | \( 1 + (-8.71 - 2.95i)T + (57.9 + 44.4i)T^{2} \) |
| 79 | \( 1 + (-1.01 + 2.05i)T + (-48.0 - 62.6i)T^{2} \) |
| 83 | \( 1 + (-0.969 + 2.34i)T + (-58.6 - 58.6i)T^{2} \) |
| 89 | \( 1 + (10.0 + 2.70i)T + (77.0 + 44.5i)T^{2} \) |
| 97 | \( 1 + (0.589 - 0.117i)T + (89.6 - 37.1i)T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−11.11998954389904600652514114895, −10.23628933934911942807483122610, −9.114339209873479268673529836987, −8.436527920005855429758669029592, −7.30005368430894024208723079758, −6.88151068367466138372261831838, −6.07708308391741994177492281641, −3.59465100971706058439153145009, −2.24079989829746388856498900404, −0.13289984070322615674875982028,
1.19909647856583066873502817395, 3.52843224074272858055486590990, 4.47760926078320191266546233181, 6.46829074625392112969995111837, 7.33708160907048500620026793146, 8.271020630837555282176705024345, 9.217717595320569944090762480377, 9.458033515053293132896268144185, 10.87232083427988670559165084034, 11.34010222121354712620664347802