↑

Properties

Label 2-2023-119.13-c0-0-3
Degree $2$
Conductor $2023$
Sign $-0.992 - 0.122i$
Analytic cond. $1.00960$
Root an. cond. $1.00479$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 0.618i·2-s + (−0.437 + 0.437i)3-s + 0.618·4-s + (−1.14 + 1.14i)5-s + (−0.270 − 0.270i)6-s + (0.707 + 0.707i)7-s + i·8-s + 0.618i·9-s + (−0.707 − 0.707i)10-s + (−0.270 + 0.270i)12-s + (−0.437 + 0.437i)14-s − i·15-s − 0.381·18-s + (−0.707 + 0.707i)20-s − 0.618·21-s + ⋯
L(s)  = 1  + 0.618i·2-s + (−0.437 + 0.437i)3-s + 0.618·4-s + (−1.14 + 1.14i)5-s + (−0.270 − 0.270i)6-s + (0.707 + 0.707i)7-s + i·8-s + 0.618i·9-s + (−0.707 − 0.707i)10-s + (−0.270 + 0.270i)12-s + (−0.437 + 0.437i)14-s − i·15-s − 0.381·18-s + (−0.707 + 0.707i)20-s − 0.618·21-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2023 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.992 - 0.122i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2023 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.992 - 0.122i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2023\)    =    \(7 \cdot 17^{2}\)
Sign: $-0.992 - 0.122i$
Analytic conductor: \(1.00960\)
Root analytic conductor: \(1.00479\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2023} (251, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2023,\ (\ :0),\ -0.992 - 0.122i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.016945019\)
\(L(\frac12)\) \(\approx\) \(1.016945019\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad7 \( 1 + (-0.707 - 0.707i)T \)
17 \( 1 \)
good2 \( 1 - 0.618iT - T^{2} \)
3 \( 1 + (0.437 - 0.437i)T - iT^{2} \)
5 \( 1 + (1.14 - 1.14i)T - iT^{2} \)
11 \( 1 - iT^{2} \)
13 \( 1 - T^{2} \)
19 \( 1 + T^{2} \)
23 \( 1 - iT^{2} \)
29 \( 1 + iT^{2} \)
31 \( 1 + (-1.14 + 1.14i)T - iT^{2} \)
37 \( 1 + iT^{2} \)
41 \( 1 + (-0.437 - 0.437i)T + iT^{2} \)
43 \( 1 + 0.618iT - T^{2} \)
47 \( 1 - T^{2} \)
53 \( 1 + 1.61iT - T^{2} \)
59 \( 1 + T^{2} \)
61 \( 1 + (-0.437 - 0.437i)T + iT^{2} \)
67 \( 1 + 1.61T + T^{2} \)
71 \( 1 + iT^{2} \)
73 \( 1 + (-0.437 + 0.437i)T - iT^{2} \)
79 \( 1 - iT^{2} \)
83 \( 1 + T^{2} \)
89 \( 1 - T^{2} \)
97 \( 1 + (1.14 - 1.14i)T - iT^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

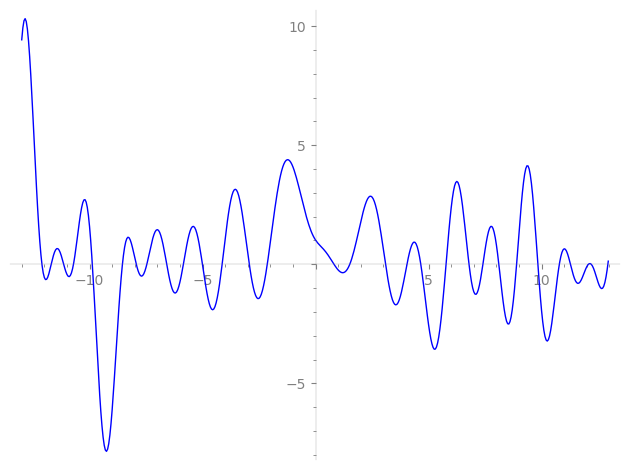
Imaginary part of the first few zeros on the critical line

−9.877007402949519265775017730382, −8.545114784425487763279296678516, −7.931559916201304835410633343117, −7.46562350377468995553287181344, −6.58436168726242501591251008036, −5.84847987924421913985047681886, −5.00540138166997621558072986210, −4.13417315133049824293595728483, −2.93134608895751081087645019986, −2.13661247610745685929725593848, 0.815682346601377710345206743160, 1.51307735651438110930992329905, 3.09724721074112509918268878020, 4.04396363523706368179835743398, 4.65523249735584340305458864214, 5.77243748381607616869396642425, 6.78969479999298516687243336678, 7.40370248833548700228464660088, 8.108578417624633101283518202098, 8.894437770606159126199391384817

Graph of the $Z$-function along the critical line