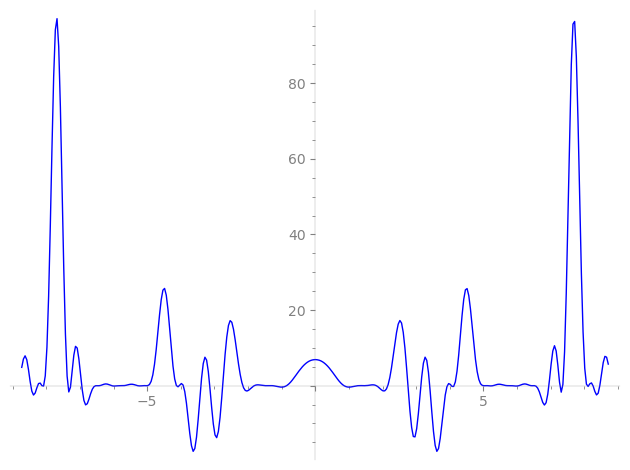
| L(s) = 1 | − 4·3-s + 8·5-s + 6·7-s + 6·9-s + 2·11-s + 18·13-s − 32·15-s + 6·17-s − 6·19-s − 24·21-s + 18·23-s + 20·25-s + 4·27-s − 6·29-s − 6·31-s − 8·33-s + 48·35-s − 10·37-s − 72·39-s + 2·41-s + 48·45-s + 6·47-s + 15·49-s − 24·51-s − 24·53-s + 16·55-s + 24·57-s + ⋯ |
| L(s) = 1 | − 2.30·3-s + 3.57·5-s + 2.26·7-s + 2·9-s + 0.603·11-s + 4.99·13-s − 8.26·15-s + 1.45·17-s − 1.37·19-s − 5.23·21-s + 3.75·23-s + 4·25-s + 0.769·27-s − 1.11·29-s − 1.07·31-s − 1.39·33-s + 8.11·35-s − 1.64·37-s − 11.5·39-s + 0.312·41-s + 7.15·45-s + 0.875·47-s + 15/7·49-s − 3.36·51-s − 3.29·53-s + 2.15·55-s + 3.17·57-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 67^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 67^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(6.898924549\) |
| \(L(\frac12)\) |
\(\approx\) |
\(6.898924549\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_2$ | \( ( 1 + 2 T + p T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - 16 T + p T^{2} )^{2} \) |
| good | 5 | $C_2$ | \( ( 1 - 2 T + p T^{2} )^{4} \) |
| 7 | $D_4\times C_2$ | \( 1 - 6 T + 3 p T^{2} - 54 T^{3} + 116 T^{4} - 54 p T^{5} + 3 p^{3} T^{6} - 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 11 | $D_4\times C_2$ | \( 1 - 2 T - 13 T^{2} + 10 T^{3} + 124 T^{4} + 10 p T^{5} - 13 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 13 | $C_2$ | \( ( 1 - 7 T + p T^{2} )^{2}( 1 - 2 T + p T^{2} )^{2} \) |
| 17 | $D_4\times C_2$ | \( 1 - 6 T + 31 T^{2} - 114 T^{3} + 276 T^{4} - 114 p T^{5} + 31 p^{2} T^{6} - 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 19 | $C_2^2$ | \( ( 1 + 3 T - 10 T^{2} + 3 p T^{3} + p^{2} T^{4} )^{2} \) |
| 23 | $D_4\times C_2$ | \( 1 - 18 T + 163 T^{2} - 990 T^{3} + 4980 T^{4} - 990 p T^{5} + 163 p^{2} T^{6} - 18 p^{3} T^{7} + p^{4} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 + 6 T + 23 T^{2} + 66 T^{3} - 372 T^{4} + 66 p T^{5} + 23 p^{2} T^{6} + 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 31 | $C_2$ | \( ( 1 - 4 T + p T^{2} )^{2}( 1 + 7 T + p T^{2} )^{2} \) |
| 37 | $D_4\times C_2$ | \( 1 + 10 T + 25 T^{2} + 10 T^{3} + 556 T^{4} + 10 p T^{5} + 25 p^{2} T^{6} + 10 p^{3} T^{7} + p^{4} T^{8} \) |
| 41 | $D_4\times C_2$ | \( 1 - 2 T - 73 T^{2} + 10 T^{3} + 4084 T^{4} + 10 p T^{5} - 73 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 43 | $D_4\times C_2$ | \( 1 - 12 T^{2} - 2410 T^{4} - 12 p^{2} T^{6} + p^{4} T^{8} \) |
| 47 | $D_4\times C_2$ | \( 1 - 6 T + 107 T^{2} - 570 T^{3} + 7380 T^{4} - 570 p T^{5} + 107 p^{2} T^{6} - 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 53 | $C_2$ | \( ( 1 + 6 T + p T^{2} )^{4} \) |
| 59 | $D_4\times C_2$ | \( 1 - 196 T^{2} + 16182 T^{4} - 196 p^{2} T^{6} + p^{4} T^{8} \) |
| 61 | $D_4\times C_2$ | \( 1 - 18 T + 225 T^{2} - 2106 T^{3} + 16556 T^{4} - 2106 p T^{5} + 225 p^{2} T^{6} - 18 p^{3} T^{7} + p^{4} T^{8} \) |
| 71 | $D_4\times C_2$ | \( 1 + 30 T + 499 T^{2} + 5970 T^{3} + 55860 T^{4} + 5970 p T^{5} + 499 p^{2} T^{6} + 30 p^{3} T^{7} + p^{4} T^{8} \) |
| 73 | $D_4\times C_2$ | \( 1 - 2 T - 119 T^{2} + 46 T^{3} + 9508 T^{4} + 46 p T^{5} - 119 p^{2} T^{6} - 2 p^{3} T^{7} + p^{4} T^{8} \) |
| 79 | $D_4\times C_2$ | \( 1 + 18 T + 261 T^{2} + 2754 T^{3} + 25700 T^{4} + 2754 p T^{5} + 261 p^{2} T^{6} + 18 p^{3} T^{7} + p^{4} T^{8} \) |
| 83 | $D_4\times C_2$ | \( 1 - 6 T + p T^{2} - 426 T^{3} - 852 T^{4} - 426 p T^{5} + p^{3} T^{6} - 6 p^{3} T^{7} + p^{4} T^{8} \) |
| 89 | $D_4\times C_2$ | \( 1 - 76 T^{2} + 3462 T^{4} - 76 p^{2} T^{6} + p^{4} T^{8} \) |
| 97 | $D_4\times C_2$ | \( 1 - 18 T + 257 T^{2} - 2682 T^{3} + 23268 T^{4} - 2682 p T^{5} + 257 p^{2} T^{6} - 18 p^{3} T^{7} + p^{4} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.27812533951935677797552538244, −6.94823660127890426684070122216, −6.52153045756498112884133662249, −6.49024574580801127004471546754, −6.41664374478398514874201280560, −6.05893219597468323138153944893, −5.82625705482552160739370610173, −5.74522908135428033398181519164, −5.73224068729256377761131635216, −5.28733761923950854152890524689, −5.12293169248337983301333947536, −5.05190018588549544553177579666, −4.99437566785758875145643318145, −4.13133153782941967027965299294, −4.04681645775054943604972298793, −3.92633620664321168583923756926, −3.40355788144005033423712426126, −3.14109714642248569359452829589, −2.75597257200193589612248917687, −2.15733390315556777864451961461, −1.81472568817702691369000931991, −1.48650017155401316263308589237, −1.43236094724480744087534942019, −1.27838303588364949801333731156, −0.853877751137873816432974287272,
0.853877751137873816432974287272, 1.27838303588364949801333731156, 1.43236094724480744087534942019, 1.48650017155401316263308589237, 1.81472568817702691369000931991, 2.15733390315556777864451961461, 2.75597257200193589612248917687, 3.14109714642248569359452829589, 3.40355788144005033423712426126, 3.92633620664321168583923756926, 4.04681645775054943604972298793, 4.13133153782941967027965299294, 4.99437566785758875145643318145, 5.05190018588549544553177579666, 5.12293169248337983301333947536, 5.28733761923950854152890524689, 5.73224068729256377761131635216, 5.74522908135428033398181519164, 5.82625705482552160739370610173, 6.05893219597468323138153944893, 6.41664374478398514874201280560, 6.49024574580801127004471546754, 6.52153045756498112884133662249, 6.94823660127890426684070122216, 7.27812533951935677797552538244