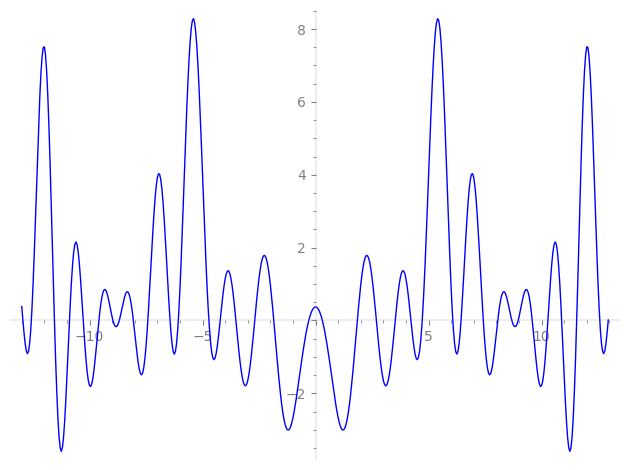
| L(s) = 1 | − 0.758·2-s + 1.52·3-s − 1.42·4-s − 5-s − 1.15·6-s − 2.88·7-s + 2.59·8-s − 0.671·9-s + 0.758·10-s − 2.17·12-s + 13-s + 2.18·14-s − 1.52·15-s + 0.876·16-s − 7.55·17-s + 0.509·18-s − 5.97·19-s + 1.42·20-s − 4.40·21-s − 4.13·23-s + 3.96·24-s + 25-s − 0.758·26-s − 5.60·27-s + 4.10·28-s + 1.16·29-s + 1.15·30-s + ⋯ |
| L(s) = 1 | − 0.536·2-s + 0.881·3-s − 0.712·4-s − 0.447·5-s − 0.472·6-s − 1.09·7-s + 0.918·8-s − 0.223·9-s + 0.239·10-s − 0.627·12-s + 0.277·13-s + 0.585·14-s − 0.393·15-s + 0.219·16-s − 1.83·17-s + 0.120·18-s − 1.37·19-s + 0.318·20-s − 0.960·21-s − 0.861·23-s + 0.809·24-s + 0.200·25-s − 0.148·26-s − 1.07·27-s + 0.776·28-s + 0.216·29-s + 0.211·30-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 7865 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 7865 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.3720825800\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.3720825800\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 5 | \( 1 + T \) |
| 11 | \( 1 \) |
| 13 | \( 1 - T \) |
| good | 2 | \( 1 + 0.758T + 2T^{2} \) |
| 3 | \( 1 - 1.52T + 3T^{2} \) |
| 7 | \( 1 + 2.88T + 7T^{2} \) |
| 17 | \( 1 + 7.55T + 17T^{2} \) |
| 19 | \( 1 + 5.97T + 19T^{2} \) |
| 23 | \( 1 + 4.13T + 23T^{2} \) |
| 29 | \( 1 - 1.16T + 29T^{2} \) |
| 31 | \( 1 - 3.42T + 31T^{2} \) |
| 37 | \( 1 - 1.26T + 37T^{2} \) |
| 41 | \( 1 - 0.324T + 41T^{2} \) |
| 43 | \( 1 - 3.69T + 43T^{2} \) |
| 47 | \( 1 + 0.687T + 47T^{2} \) |
| 53 | \( 1 + 7.22T + 53T^{2} \) |
| 59 | \( 1 + 14.8T + 59T^{2} \) |
| 61 | \( 1 + 3.05T + 61T^{2} \) |
| 67 | \( 1 - 14.4T + 67T^{2} \) |
| 71 | \( 1 + 3.70T + 71T^{2} \) |
| 73 | \( 1 + 14.6T + 73T^{2} \) |
| 79 | \( 1 + 16.1T + 79T^{2} \) |
| 83 | \( 1 - 14.8T + 83T^{2} \) |
| 89 | \( 1 - 9.83T + 89T^{2} \) |
| 97 | \( 1 - 3.84T + 97T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.061056783750201821178856049116, −7.42070428857475486832606598064, −6.43717164576232175949713004442, −6.07224089650845568758452581233, −4.71894870200139899806364547742, −4.21966801888771836763937224258, −3.52473580325154431979764607895, −2.69092244371208999029168847530, −1.84833584371155990325450919162, −0.30012872096613817253142808189,
0.30012872096613817253142808189, 1.84833584371155990325450919162, 2.69092244371208999029168847530, 3.52473580325154431979764607895, 4.21966801888771836763937224258, 4.71894870200139899806364547742, 6.07224089650845568758452581233, 6.43717164576232175949713004442, 7.42070428857475486832606598064, 8.061056783750201821178856049116