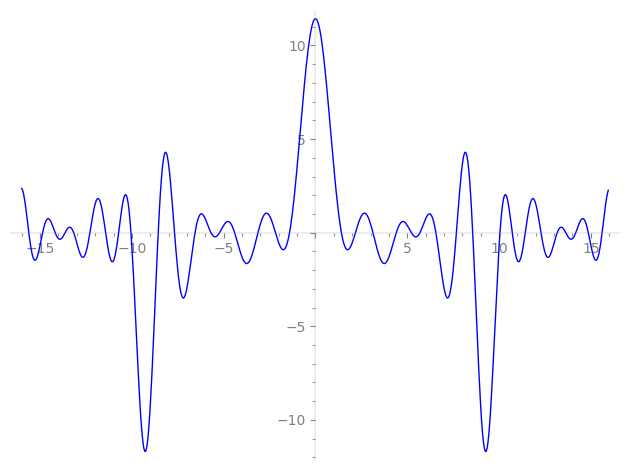
| L(s) = 1 | + 10.2·2-s + 73.9·4-s + 72.1·5-s + 169.·7-s + 431.·8-s + 742.·10-s − 474.·11-s + 556.·13-s + 1.74e3·14-s + 2.07e3·16-s + 503.·17-s − 3.03·19-s + 5.32e3·20-s − 4.88e3·22-s − 599.·23-s + 2.07e3·25-s + 5.72e3·26-s + 1.25e4·28-s + 5.48e3·29-s − 3.41e3·31-s + 7.53e3·32-s + 5.18e3·34-s + 1.22e4·35-s + 4.79e3·37-s − 31.2·38-s + 3.11e4·40-s − 8.92e3·41-s + ⋯ |
| L(s) = 1 | + 1.81·2-s + 2.30·4-s + 1.28·5-s + 1.31·7-s + 2.38·8-s + 2.34·10-s − 1.18·11-s + 0.912·13-s + 2.38·14-s + 2.02·16-s + 0.422·17-s − 0.00192·19-s + 2.97·20-s − 2.15·22-s − 0.236·23-s + 0.663·25-s + 1.66·26-s + 3.02·28-s + 1.21·29-s − 0.638·31-s + 1.30·32-s + 0.769·34-s + 1.69·35-s + 0.576·37-s − 0.00350·38-s + 3.07·40-s − 0.829·41-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 729 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(6-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 729 ^{s/2} \, \Gamma_{\C}(s+5/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(3)\) |
\(\approx\) |
\(11.43376970\) |
| \(L(\frac12)\) |
\(\approx\) |
\(11.43376970\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 3 | \( 1 \) |
| good | 2 | \( 1 - 10.2T + 32T^{2} \) |
| 5 | \( 1 - 72.1T + 3.12e3T^{2} \) |
| 7 | \( 1 - 169.T + 1.68e4T^{2} \) |
| 11 | \( 1 + 474.T + 1.61e5T^{2} \) |
| 13 | \( 1 - 556.T + 3.71e5T^{2} \) |
| 17 | \( 1 - 503.T + 1.41e6T^{2} \) |
| 19 | \( 1 + 3.03T + 2.47e6T^{2} \) |
| 23 | \( 1 + 599.T + 6.43e6T^{2} \) |
| 29 | \( 1 - 5.48e3T + 2.05e7T^{2} \) |
| 31 | \( 1 + 3.41e3T + 2.86e7T^{2} \) |
| 37 | \( 1 - 4.79e3T + 6.93e7T^{2} \) |
| 41 | \( 1 + 8.92e3T + 1.15e8T^{2} \) |
| 43 | \( 1 + 1.81e4T + 1.47e8T^{2} \) |
| 47 | \( 1 - 1.99e4T + 2.29e8T^{2} \) |
| 53 | \( 1 + 1.04e4T + 4.18e8T^{2} \) |
| 59 | \( 1 + 1.05e4T + 7.14e8T^{2} \) |
| 61 | \( 1 - 1.06e4T + 8.44e8T^{2} \) |
| 67 | \( 1 - 1.77e3T + 1.35e9T^{2} \) |
| 71 | \( 1 - 4.37e4T + 1.80e9T^{2} \) |
| 73 | \( 1 + 8.62e4T + 2.07e9T^{2} \) |
| 79 | \( 1 + 6.82e4T + 3.07e9T^{2} \) |
| 83 | \( 1 - 7.75e4T + 3.93e9T^{2} \) |
| 89 | \( 1 + 4.28e4T + 5.58e9T^{2} \) |
| 97 | \( 1 + 1.86e4T + 8.58e9T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−10.05082135586845598369713404861, −8.565642821376797423137181716905, −7.67711490978984928993878786063, −6.56028767232854935232984991216, −5.69271759059524900453625034768, −5.22427715009140937986692143487, −4.40245616122873247531807027331, −3.13179897405721199852000917752, −2.17778996931717396108195250884, −1.41306619266585403636699082594,
1.41306619266585403636699082594, 2.17778996931717396108195250884, 3.13179897405721199852000917752, 4.40245616122873247531807027331, 5.22427715009140937986692143487, 5.69271759059524900453625034768, 6.56028767232854935232984991216, 7.67711490978984928993878786063, 8.565642821376797423137181716905, 10.05082135586845598369713404861