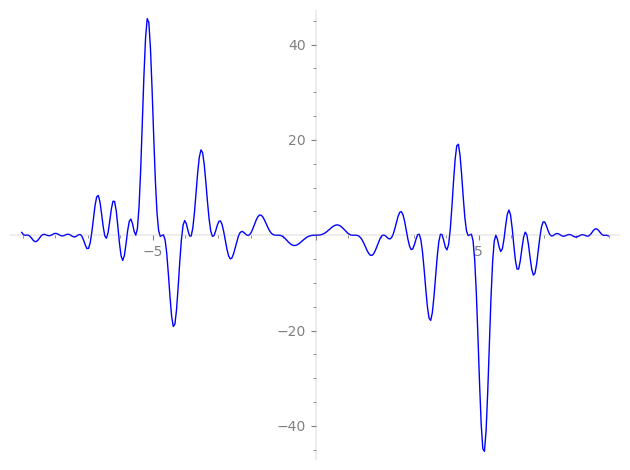
| L(s) = 1 | − 3·2-s + 6·4-s − 3·5-s + 3·7-s − 10·8-s + 9·10-s − 3·11-s + 2·13-s − 9·14-s + 15·16-s − 2·17-s − 18·20-s + 9·22-s − 4·23-s + 6·25-s − 6·26-s + 18·28-s − 2·29-s − 4·31-s − 21·32-s + 6·34-s − 9·35-s + 6·37-s + 30·40-s + 6·41-s − 18·44-s + 12·46-s + ⋯ |
| L(s) = 1 | − 2.12·2-s + 3·4-s − 1.34·5-s + 1.13·7-s − 3.53·8-s + 2.84·10-s − 0.904·11-s + 0.554·13-s − 2.40·14-s + 15/4·16-s − 0.485·17-s − 4.02·20-s + 1.91·22-s − 0.834·23-s + 6/5·25-s − 1.17·26-s + 3.40·28-s − 0.371·29-s − 0.718·31-s − 3.71·32-s + 1.02·34-s − 1.52·35-s + 0.986·37-s + 4.74·40-s + 0.937·41-s − 2.71·44-s + 1.76·46-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{3} \cdot 3^{6} \cdot 5^{3} \cdot 7^{3} \cdot 11^{3}\right)^{s/2} \, \Gamma_{\C}(s)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{3} \cdot 3^{6} \cdot 5^{3} \cdot 7^{3} \cdot 11^{3}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_1$ | \( ( 1 + T )^{3} \) |
| 3 | | \( 1 \) |
| 5 | $C_1$ | \( ( 1 + T )^{3} \) |
| 7 | $C_1$ | \( ( 1 - T )^{3} \) |
| 11 | $C_1$ | \( ( 1 + T )^{3} \) |
| good | 13 | $S_4\times C_2$ | \( 1 - 2 T + 19 T^{2} - 44 T^{3} + 19 p T^{4} - 2 p^{2} T^{5} + p^{3} T^{6} \) |
| 17 | $S_4\times C_2$ | \( 1 + 2 T + 15 T^{2} - 36 T^{3} + 15 p T^{4} + 2 p^{2} T^{5} + p^{3} T^{6} \) |
| 19 | $C_2$ | \( ( 1 + p T^{2} )^{3} \) |
| 23 | $S_4\times C_2$ | \( 1 + 4 T + 37 T^{2} + 216 T^{3} + 37 p T^{4} + 4 p^{2} T^{5} + p^{3} T^{6} \) |
| 29 | $S_4\times C_2$ | \( 1 + 2 T + 35 T^{2} + 76 T^{3} + 35 p T^{4} + 2 p^{2} T^{5} + p^{3} T^{6} \) |
| 31 | $S_4\times C_2$ | \( 1 + 4 T + 13 T^{2} + 184 T^{3} + 13 p T^{4} + 4 p^{2} T^{5} + p^{3} T^{6} \) |
| 37 | $S_4\times C_2$ | \( 1 - 6 T + 11 T^{2} + 188 T^{3} + 11 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 41 | $S_4\times C_2$ | \( 1 - 6 T + 71 T^{2} - 244 T^{3} + 71 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 43 | $S_4\times C_2$ | \( 1 + 65 T^{2} - 128 T^{3} + 65 p T^{4} + p^{3} T^{6} \) |
| 47 | $S_4\times C_2$ | \( 1 + 4 T + 61 T^{2} + 312 T^{3} + 61 p T^{4} + 4 p^{2} T^{5} + p^{3} T^{6} \) |
| 53 | $S_4\times C_2$ | \( 1 - 6 T + 107 T^{2} - 644 T^{3} + 107 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 59 | $S_4\times C_2$ | \( 1 + 12 T + 161 T^{2} + 1096 T^{3} + 161 p T^{4} + 12 p^{2} T^{5} + p^{3} T^{6} \) |
| 61 | $S_4\times C_2$ | \( 1 + 10 T + 67 T^{2} + 124 T^{3} + 67 p T^{4} + 10 p^{2} T^{5} + p^{3} T^{6} \) |
| 67 | $S_4\times C_2$ | \( 1 + 41 T^{2} + 608 T^{3} + 41 p T^{4} + p^{3} T^{6} \) |
| 71 | $S_4\times C_2$ | \( 1 + 4 T + 165 T^{2} + 504 T^{3} + 165 p T^{4} + 4 p^{2} T^{5} + p^{3} T^{6} \) |
| 73 | $S_4\times C_2$ | \( 1 + 10 T + 39 T^{2} - 404 T^{3} + 39 p T^{4} + 10 p^{2} T^{5} + p^{3} T^{6} \) |
| 79 | $S_4\times C_2$ | \( 1 + 4 T + 29 T^{2} + 312 T^{3} + 29 p T^{4} + 4 p^{2} T^{5} + p^{3} T^{6} \) |
| 83 | $S_4\times C_2$ | \( 1 + 185 T^{2} + 128 T^{3} + 185 p T^{4} + p^{3} T^{6} \) |
| 89 | $S_4\times C_2$ | \( 1 - 2 T + 135 T^{2} + 324 T^{3} + 135 p T^{4} - 2 p^{2} T^{5} + p^{3} T^{6} \) |
| 97 | $C_2$ | \( ( 1 + 2 T + p T^{2} )^{3} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{6} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.51979833526576526678337178740, −7.30273195568147684981422558303, −7.19846954692372315595616161212, −6.88532251683015697954255188071, −6.47980837476769764624557873208, −6.39045197596355537506379447486, −6.04855613141405099495610881384, −5.79131794027924534168186832233, −5.53074429834681490201381344318, −5.52059753677908371676234428195, −4.79282752824016769022844153337, −4.71513740129664447027237316029, −4.66389810110819910146621445572, −4.11102410614688080519400672727, −3.88312744719765326484459753210, −3.81468489467178277191254098710, −3.19098257053126696142369606941, −3.11708358123281205142413101204, −2.80475113877757307053034755550, −2.36357330680934762160469011623, −2.10956536817677296025941825942, −2.05160956713319323601729760311, −1.23907381686692399012964099751, −1.20571198737808673268269841227, −1.11353582930563265465868718428, 0, 0, 0,
1.11353582930563265465868718428, 1.20571198737808673268269841227, 1.23907381686692399012964099751, 2.05160956713319323601729760311, 2.10956536817677296025941825942, 2.36357330680934762160469011623, 2.80475113877757307053034755550, 3.11708358123281205142413101204, 3.19098257053126696142369606941, 3.81468489467178277191254098710, 3.88312744719765326484459753210, 4.11102410614688080519400672727, 4.66389810110819910146621445572, 4.71513740129664447027237316029, 4.79282752824016769022844153337, 5.52059753677908371676234428195, 5.53074429834681490201381344318, 5.79131794027924534168186832233, 6.04855613141405099495610881384, 6.39045197596355537506379447486, 6.47980837476769764624557873208, 6.88532251683015697954255188071, 7.19846954692372315595616161212, 7.30273195568147684981422558303, 7.51979833526576526678337178740