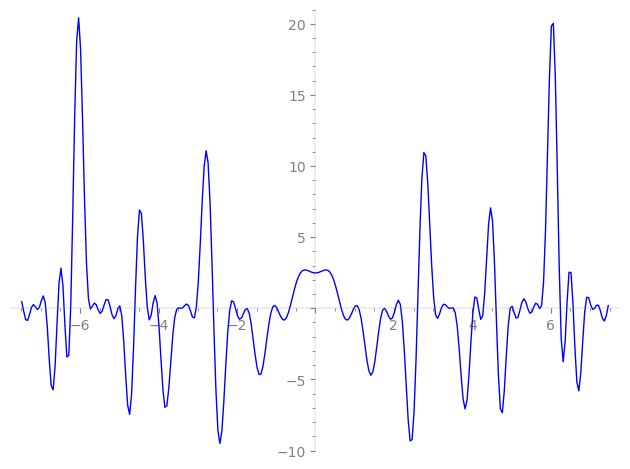
| L(s) = 1 | + 9-s + 4·19-s − 4·31-s − 49-s + 2·61-s + 4·79-s + 4·109-s − 2·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 169-s + 4·171-s + 173-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + ⋯ |
| L(s) = 1 | + 9-s + 4·19-s − 4·31-s − 49-s + 2·61-s + 4·79-s + 4·109-s − 2·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 169-s + 4·171-s + 173-s + 179-s + 181-s + 191-s + 193-s + 197-s + 199-s + 211-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 3^{4} \cdot 5^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(2.480547867\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.480547867\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| 5 | | \( 1 \) |
| 13 | $C_2^2$ | \( 1 - T^{2} + T^{4} \) |
| good | 7 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 11 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 17 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 19 | $C_2$ | \( ( 1 - T + T^{2} )^{4} \) |
| 23 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 29 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 31 | $C_2$ | \( ( 1 + T + T^{2} )^{4} \) |
| 37 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 41 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 43 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 47 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 53 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 59 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 61 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 67 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 71 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 - T^{2} + T^{4} )^{2} \) |
| 79 | $C_2$ | \( ( 1 - T + T^{2} )^{4} \) |
| 83 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 89 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 97 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.23868542212858611176200805497, −5.74791703983566884532058347046, −5.70830185504119736654106332588, −5.55350149632994990400412426483, −5.41039796952086160572971188511, −5.22456062722578984995285376400, −5.03357123568392203288749425860, −4.96447742024044496769741766194, −4.60288350498604738757894019457, −4.28460245655599157000234279068, −4.15805379428523416800960555040, −4.02266624640152278932935022076, −3.52056204233690099996045639511, −3.44837392622569684206313922335, −3.40105676053562591283743019230, −3.20757621463677904374184490553, −3.03854603575041572333902208271, −2.60312525979828824668957178513, −2.17916084578003895649845008743, −2.03874594373791569994623177968, −1.75516384687044574321441458248, −1.75017894614983997799018382633, −1.10255609849569855206010191839, −0.979051606403812022048438441215, −0.65661728146322750035283375383,
0.65661728146322750035283375383, 0.979051606403812022048438441215, 1.10255609849569855206010191839, 1.75017894614983997799018382633, 1.75516384687044574321441458248, 2.03874594373791569994623177968, 2.17916084578003895649845008743, 2.60312525979828824668957178513, 3.03854603575041572333902208271, 3.20757621463677904374184490553, 3.40105676053562591283743019230, 3.44837392622569684206313922335, 3.52056204233690099996045639511, 4.02266624640152278932935022076, 4.15805379428523416800960555040, 4.28460245655599157000234279068, 4.60288350498604738757894019457, 4.96447742024044496769741766194, 5.03357123568392203288749425860, 5.22456062722578984995285376400, 5.41039796952086160572971188511, 5.55350149632994990400412426483, 5.70830185504119736654106332588, 5.74791703983566884532058347046, 6.23868542212858611176200805497