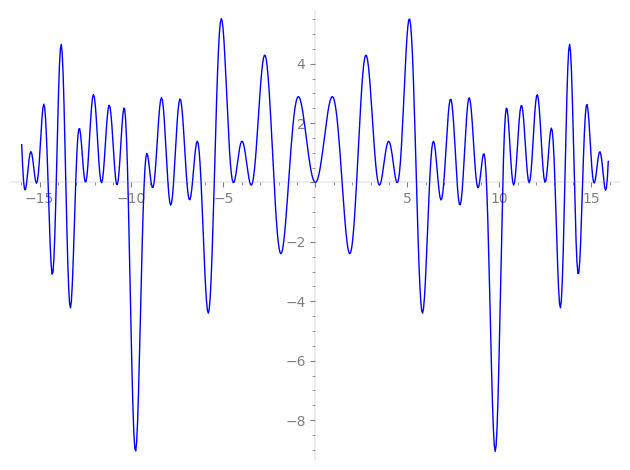
| L(s) = 1 | − 18·5-s − 8·7-s + 36·11-s + 10·13-s − 36·17-s − 200·19-s + 72·23-s + 125·25-s − 234·29-s + 16·31-s + 144·35-s − 452·37-s + 90·41-s − 452·43-s + 432·47-s + 343·49-s − 828·53-s − 648·55-s − 684·59-s − 422·61-s − 180·65-s − 332·67-s + 720·71-s + 52·73-s − 288·77-s − 512·79-s − 1.18e3·83-s + ⋯ |
| L(s) = 1 | − 1.60·5-s − 0.431·7-s + 0.986·11-s + 0.213·13-s − 0.513·17-s − 2.41·19-s + 0.652·23-s + 25-s − 1.49·29-s + 0.0926·31-s + 0.695·35-s − 2.00·37-s + 0.342·41-s − 1.60·43-s + 1.34·47-s + 49-s − 2.14·53-s − 1.58·55-s − 1.50·59-s − 0.885·61-s − 0.343·65-s − 0.605·67-s + 1.20·71-s + 0.0833·73-s − 0.426·77-s − 0.729·79-s − 1.57·83-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 104976 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 104976 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(2)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| good | 5 | $C_2^2$ | \( 1 + 18 T + 199 T^{2} + 18 p^{3} T^{3} + p^{6} T^{4} \) |
| 7 | $C_2^2$ | \( 1 + 8 T - 279 T^{2} + 8 p^{3} T^{3} + p^{6} T^{4} \) |
| 11 | $C_2^2$ | \( 1 - 36 T - 35 T^{2} - 36 p^{3} T^{3} + p^{6} T^{4} \) |
| 13 | $C_2^2$ | \( 1 - 10 T - 2097 T^{2} - 10 p^{3} T^{3} + p^{6} T^{4} \) |
| 17 | $C_2$ | \( ( 1 + 18 T + p^{3} T^{2} )^{2} \) |
| 19 | $C_2$ | \( ( 1 + 100 T + p^{3} T^{2} )^{2} \) |
| 23 | $C_2^2$ | \( 1 - 72 T - 6983 T^{2} - 72 p^{3} T^{3} + p^{6} T^{4} \) |
| 29 | $C_2^2$ | \( 1 + 234 T + 30367 T^{2} + 234 p^{3} T^{3} + p^{6} T^{4} \) |
| 31 | $C_2^2$ | \( 1 - 16 T - 29535 T^{2} - 16 p^{3} T^{3} + p^{6} T^{4} \) |
| 37 | $C_2$ | \( ( 1 + 226 T + p^{3} T^{2} )^{2} \) |
| 41 | $C_2^2$ | \( 1 - 90 T - 60821 T^{2} - 90 p^{3} T^{3} + p^{6} T^{4} \) |
| 43 | $C_2^2$ | \( 1 + 452 T + 124797 T^{2} + 452 p^{3} T^{3} + p^{6} T^{4} \) |
| 47 | $C_2^2$ | \( 1 - 432 T + 82801 T^{2} - 432 p^{3} T^{3} + p^{6} T^{4} \) |
| 53 | $C_2$ | \( ( 1 + 414 T + p^{3} T^{2} )^{2} \) |
| 59 | $C_2^2$ | \( 1 + 684 T + 262477 T^{2} + 684 p^{3} T^{3} + p^{6} T^{4} \) |
| 61 | $C_2^2$ | \( 1 + 422 T - 48897 T^{2} + 422 p^{3} T^{3} + p^{6} T^{4} \) |
| 67 | $C_2^2$ | \( 1 + 332 T - 190539 T^{2} + 332 p^{3} T^{3} + p^{6} T^{4} \) |
| 71 | $C_2$ | \( ( 1 - 360 T + p^{3} T^{2} )^{2} \) |
| 73 | $C_2$ | \( ( 1 - 26 T + p^{3} T^{2} )^{2} \) |
| 79 | $C_2^2$ | \( 1 + 512 T - 230895 T^{2} + 512 p^{3} T^{3} + p^{6} T^{4} \) |
| 83 | $C_2^2$ | \( 1 + 1188 T + 839557 T^{2} + 1188 p^{3} T^{3} + p^{6} T^{4} \) |
| 89 | $C_2$ | \( ( 1 - 630 T + p^{3} T^{2} )^{2} \) |
| 97 | $C_2^2$ | \( 1 - 1054 T + 198243 T^{2} - 1054 p^{3} T^{3} + p^{6} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−10.83424097124165793134393736530, −10.73853287673954617269323677771, −10.19654369423144681302239975724, −9.307547538123566023498884367750, −8.930998785315700811138168964847, −8.769378165223303546761876182299, −8.017185507758760957633677608508, −7.71095089543020084460753617303, −6.98503989643137200029833562190, −6.68372067474497949575620304304, −6.21448453346420236943158412481, −5.49874255140450193148474317013, −4.47560117966489706225804945176, −4.42807257478413394746059578834, −3.56312585870681463522394508650, −3.41298218900240172364526820560, −2.24295913081658819090944787102, −1.45726786870607816565944993370, 0, 0,
1.45726786870607816565944993370, 2.24295913081658819090944787102, 3.41298218900240172364526820560, 3.56312585870681463522394508650, 4.42807257478413394746059578834, 4.47560117966489706225804945176, 5.49874255140450193148474317013, 6.21448453346420236943158412481, 6.68372067474497949575620304304, 6.98503989643137200029833562190, 7.71095089543020084460753617303, 8.017185507758760957633677608508, 8.769378165223303546761876182299, 8.930998785315700811138168964847, 9.307547538123566023498884367750, 10.19654369423144681302239975724, 10.73853287673954617269323677771, 10.83424097124165793134393736530