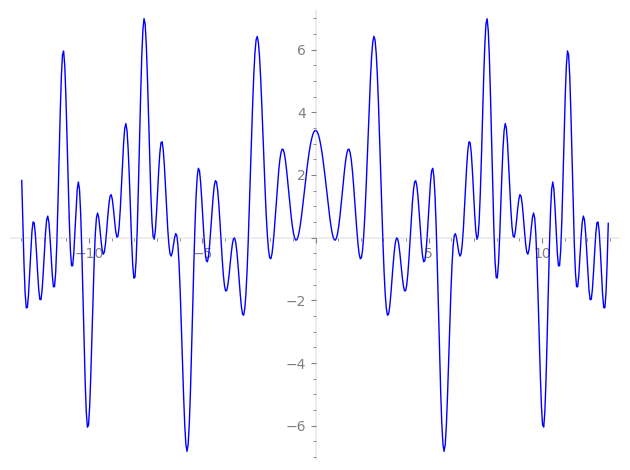
| L(s) = 1 | − 4-s + 8·11-s + 16-s + 20·29-s − 16·31-s + 4·41-s − 8·44-s − 49-s + 8·59-s − 12·61-s − 64-s + 24·71-s + 16·79-s + 28·89-s + 12·101-s + 36·109-s − 20·116-s + 26·121-s + 16·124-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + ⋯ |
| L(s) = 1 | − 1/2·4-s + 2.41·11-s + 1/4·16-s + 3.71·29-s − 2.87·31-s + 0.624·41-s − 1.20·44-s − 1/7·49-s + 1.04·59-s − 1.53·61-s − 1/8·64-s + 2.84·71-s + 1.80·79-s + 2.96·89-s + 1.19·101-s + 3.44·109-s − 1.85·116-s + 2.36·121-s + 1.43·124-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 9922500 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 9922500 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(3.426499116\) |
| \(L(\frac12)\) |
\(\approx\) |
\(3.426499116\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( 1 + T^{2} \) |
| 3 | | \( 1 \) |
| 5 | | \( 1 \) |
| 7 | $C_2$ | \( 1 + T^{2} \) |
| good | 11 | $C_2$ | \( ( 1 - 4 T + p T^{2} )^{2} \) |
| 13 | $C_2^2$ | \( 1 - 22 T^{2} + p^{2} T^{4} \) |
| 17 | $C_2^2$ | \( 1 + 2 T^{2} + p^{2} T^{4} \) |
| 19 | $C_2$ | \( ( 1 + p T^{2} )^{2} \) |
| 23 | $C_2^2$ | \( 1 + 18 T^{2} + p^{2} T^{4} \) |
| 29 | $C_2$ | \( ( 1 - 10 T + p T^{2} )^{2} \) |
| 31 | $C_2$ | \( ( 1 + 8 T + p T^{2} )^{2} \) |
| 37 | $C_2$ | \( ( 1 - 12 T + p T^{2} )( 1 + 12 T + p T^{2} ) \) |
| 41 | $C_2$ | \( ( 1 - 2 T + p T^{2} )^{2} \) |
| 43 | $C_2^2$ | \( 1 - 22 T^{2} + p^{2} T^{4} \) |
| 47 | $C_2^2$ | \( 1 - 78 T^{2} + p^{2} T^{4} \) |
| 53 | $C_2^2$ | \( 1 - 6 T^{2} + p^{2} T^{4} \) |
| 59 | $C_2$ | \( ( 1 - 4 T + p T^{2} )^{2} \) |
| 61 | $C_2$ | \( ( 1 + 6 T + p T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - p T^{2} )^{2} \) |
| 71 | $C_2$ | \( ( 1 - 12 T + p T^{2} )^{2} \) |
| 73 | $C_2$ | \( ( 1 - 16 T + p T^{2} )( 1 + 16 T + p T^{2} ) \) |
| 79 | $C_2$ | \( ( 1 - 8 T + p T^{2} )^{2} \) |
| 83 | $C_2^2$ | \( 1 - 150 T^{2} + p^{2} T^{4} \) |
| 89 | $C_2$ | \( ( 1 - 14 T + p T^{2} )^{2} \) |
| 97 | $C_2^2$ | \( 1 - 190 T^{2} + p^{2} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.762485760516814276506416481264, −8.749491786643779186228267231118, −8.128339392213194433757424584729, −7.88531183134421312445158632349, −7.16640032452598025229564295112, −7.10919006723036228969870917074, −6.50124166124116258540171234323, −6.22404062695061627230518680314, −6.10994024603543478578020940917, −5.34101421649244286684639540018, −4.92487744699090108147806507829, −4.65236891331094227497641237193, −4.18004133837923729013381197563, −3.60074446134783753497241225253, −3.58378121644805737314205261849, −2.96796623091637426906950349012, −2.12109098891343464276410383978, −1.84880430456966005618753217806, −0.927936750808387808129664658783, −0.78461377901731977779196383475,
0.78461377901731977779196383475, 0.927936750808387808129664658783, 1.84880430456966005618753217806, 2.12109098891343464276410383978, 2.96796623091637426906950349012, 3.58378121644805737314205261849, 3.60074446134783753497241225253, 4.18004133837923729013381197563, 4.65236891331094227497641237193, 4.92487744699090108147806507829, 5.34101421649244286684639540018, 6.10994024603543478578020940917, 6.22404062695061627230518680314, 6.50124166124116258540171234323, 7.10919006723036228969870917074, 7.16640032452598025229564295112, 7.88531183134421312445158632349, 8.128339392213194433757424584729, 8.749491786643779186228267231118, 8.762485760516814276506416481264