| L(s) = 1 | + 2·3-s + 4·4-s + 7-s + 9-s + 8·12-s − 13-s + 10·16-s + 19-s + 2·21-s − 2·25-s − 2·27-s + 4·28-s + 4·36-s − 37-s − 2·39-s − 43-s + 20·48-s + 49-s − 4·52-s + 2·57-s + 2·61-s + 63-s + 20·64-s + 67-s − 73-s − 4·75-s + 4·76-s + ⋯ |
| L(s) = 1 | + 2·3-s + 4·4-s + 7-s + 9-s + 8·12-s − 13-s + 10·16-s + 19-s + 2·21-s − 2·25-s − 2·27-s + 4·28-s + 4·36-s − 37-s − 2·39-s − 43-s + 20·48-s + 49-s − 4·52-s + 2·57-s + 2·61-s + 63-s + 20·64-s + 67-s − 73-s − 4·75-s + 4·76-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 31^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 31^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(11.64944597\) |
| \(L(\frac12)\) |
\(\approx\) |
\(11.64944597\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 3 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 31 | | \( 1 \) |
| good | 2 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 5 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 7 | $C_4\times C_2$ | \( 1 - T + T^{3} - T^{4} + T^{5} - T^{7} + T^{8} \) |
| 11 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 13 | $C_4\times C_2$ | \( 1 + T - T^{3} - T^{4} - T^{5} + T^{7} + T^{8} \) |
| 17 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 19 | $C_4\times C_2$ | \( 1 - T + T^{3} - T^{4} + T^{5} - T^{7} + T^{8} \) |
| 23 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 29 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 37 | $C_4\times C_2$ | \( 1 + T - T^{3} - T^{4} - T^{5} + T^{7} + T^{8} \) |
| 41 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 43 | $C_4\times C_2$ | \( 1 + T - T^{3} - T^{4} - T^{5} + T^{7} + T^{8} \) |
| 47 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 53 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 59 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 61 | $C_4$ | \( ( 1 - T + T^{2} - T^{3} + T^{4} )^{2} \) |
| 67 | $C_4\times C_2$ | \( 1 - T + T^{3} - T^{4} + T^{5} - T^{7} + T^{8} \) |
| 71 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 73 | $C_4\times C_2$ | \( 1 + T - T^{3} - T^{4} - T^{5} + T^{7} + T^{8} \) |
| 79 | $C_4\times C_2$ | \( 1 + T - T^{3} - T^{4} - T^{5} + T^{7} + T^{8} \) |
| 83 | $C_2$ | \( ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2} \) |
| 89 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 97 | $C_4$ | \( ( 1 + T + T^{2} + T^{3} + T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
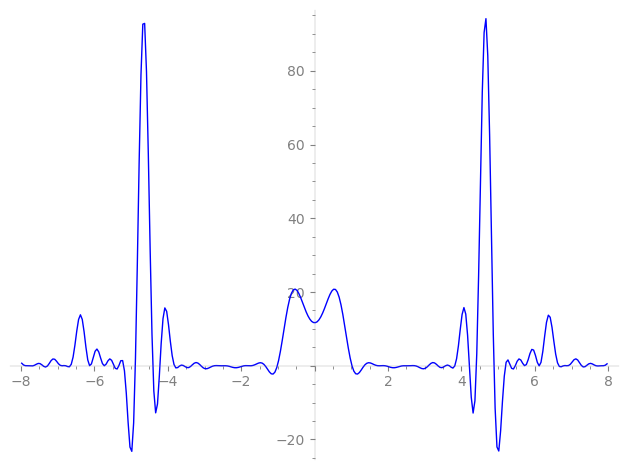
Imaginary part of the first few zeros on the critical line
−6.65178131888186445211632935896, −6.12984138892570850837899311394, −6.11143029717960571168313149907, −5.73446132254347911490935766187, −5.72648802451290532709877088875, −5.46752956099092504322238041429, −5.33482320956236270498058127442, −5.20005867571978764589651700069, −4.88684229121382040607593207122, −4.40805970154516567454665185292, −4.21646364595958317774311483032, −3.82051502018409079458829175889, −3.67100109962997912643688113428, −3.56664128045689956330690632641, −3.35873048892368180947563464811, −3.09894491594962057300634086381, −2.73628733802795498688653071978, −2.59370304921240172669784540960, −2.48879222199384426746535480917, −2.42699300375549371635289576143, −1.91567279256723325850775734848, −1.79132471176815784913935094854, −1.72961070521057083969756575444, −1.34881688111813669497844332958, −1.01744785319254563633680935866,
1.01744785319254563633680935866, 1.34881688111813669497844332958, 1.72961070521057083969756575444, 1.79132471176815784913935094854, 1.91567279256723325850775734848, 2.42699300375549371635289576143, 2.48879222199384426746535480917, 2.59370304921240172669784540960, 2.73628733802795498688653071978, 3.09894491594962057300634086381, 3.35873048892368180947563464811, 3.56664128045689956330690632641, 3.67100109962997912643688113428, 3.82051502018409079458829175889, 4.21646364595958317774311483032, 4.40805970154516567454665185292, 4.88684229121382040607593207122, 5.20005867571978764589651700069, 5.33482320956236270498058127442, 5.46752956099092504322238041429, 5.72648802451290532709877088875, 5.73446132254347911490935766187, 6.11143029717960571168313149907, 6.12984138892570850837899311394, 6.65178131888186445211632935896