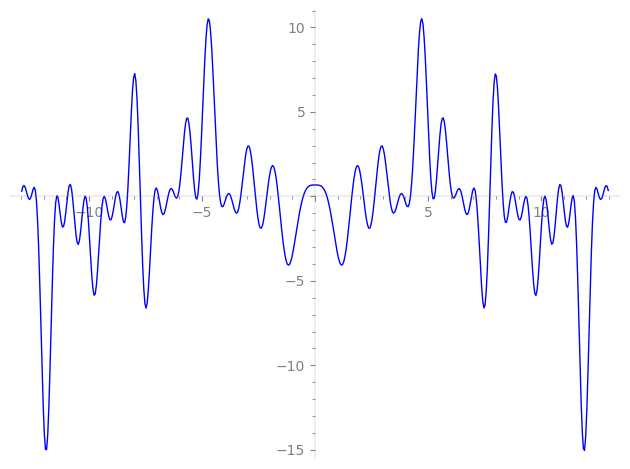
| L(s) = 1 | − 2·7-s + 2·13-s − 16-s − 2·19-s − 2·31-s − 2·37-s + 2·43-s + 49-s + 2·61-s + 2·67-s − 4·91-s + 2·97-s − 2·103-s + 2·112-s + 2·121-s + 127-s + 131-s + 4·133-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 169-s + 173-s + ⋯ |
| L(s) = 1 | − 2·7-s + 2·13-s − 16-s − 2·19-s − 2·31-s − 2·37-s + 2·43-s + 49-s + 2·61-s + 2·67-s − 4·91-s + 2·97-s − 2·103-s + 2·112-s + 2·121-s + 127-s + 131-s + 4·133-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 169-s + 173-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 6765201 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 6765201 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.6755722881\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.6755722881\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 3 | | \( 1 \) |
| 17 | | \( 1 \) |
| good | 2 | $C_2^2$ | \( 1 + T^{4} \) |
| 5 | $C_2^2$ | \( 1 + T^{4} \) |
| 7 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 11 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 13 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 19 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 23 | $C_2^2$ | \( 1 + T^{4} \) |
| 29 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 31 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 37 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 41 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 43 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 47 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 53 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 59 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 61 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| 71 | $C_2^2$ | \( 1 + T^{4} \) |
| 73 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 79 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 83 | $C_2^2$ | \( 1 + T^{4} \) |
| 89 | $C_2^2$ | \( 1 + T^{4} \) |
| 97 | $C_2$ | \( ( 1 - T + T^{2} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.326834246147090560417409749285, −8.823622256987809291614457058669, −8.657425953427082792199055691332, −8.301957838272685982792047386375, −7.72886470812827842660007750560, −7.11969637538421973167195938367, −6.92108683010153937643509465332, −6.50489665714416548170838749884, −6.19492924055178569594315718508, −6.07578726019765806425117292528, −5.29041936353379094595219217218, −5.19598753866712259227529533919, −4.21876732337717896777955879124, −3.91299959990558752207192893875, −3.73218600285115517355251786864, −3.29053314577641316694381223089, −2.63757267510790531800466216855, −2.13787381217851492620682795108, −1.62612481992632372434840412922, −0.52327681997133934574765767505,
0.52327681997133934574765767505, 1.62612481992632372434840412922, 2.13787381217851492620682795108, 2.63757267510790531800466216855, 3.29053314577641316694381223089, 3.73218600285115517355251786864, 3.91299959990558752207192893875, 4.21876732337717896777955879124, 5.19598753866712259227529533919, 5.29041936353379094595219217218, 6.07578726019765806425117292528, 6.19492924055178569594315718508, 6.50489665714416548170838749884, 6.92108683010153937643509465332, 7.11969637538421973167195938367, 7.72886470812827842660007750560, 8.301957838272685982792047386375, 8.657425953427082792199055691332, 8.823622256987809291614457058669, 9.326834246147090560417409749285