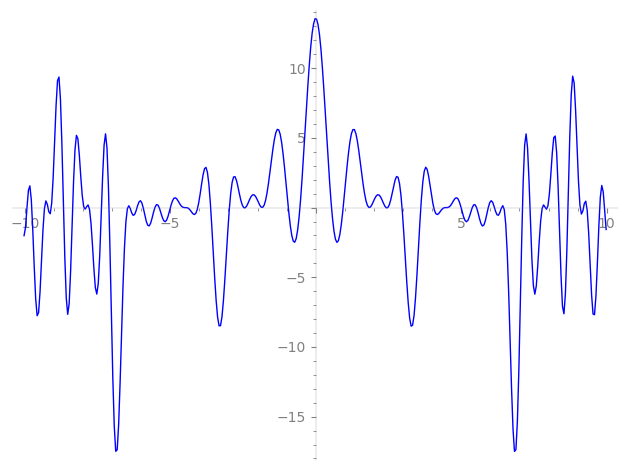
| L(s) = 1 | + 4·2-s + 4·4-s + 14·5-s + 45·7-s − 16·8-s + 56·10-s + 5·11-s − 35·13-s + 180·14-s − 64·16-s − 130·17-s − 3·19-s + 56·20-s + 20·22-s + 33·23-s − 269·25-s − 140·26-s + 180·28-s − 198·29-s + 560·31-s − 64·32-s − 520·34-s + 630·35-s + 702·37-s − 12·38-s − 224·40-s + 242·41-s + ⋯ |
| L(s) = 1 | + 1.41·2-s + 1/2·4-s + 1.25·5-s + 2.42·7-s − 0.707·8-s + 1.77·10-s + 0.137·11-s − 0.746·13-s + 3.43·14-s − 16-s − 1.85·17-s − 0.0362·19-s + 0.626·20-s + 0.193·22-s + 0.299·23-s − 2.15·25-s − 1.05·26-s + 1.21·28-s − 1.26·29-s + 3.24·31-s − 0.353·32-s − 2.62·34-s + 3.04·35-s + 3.11·37-s − 0.0512·38-s − 0.885·40-s + 0.921·41-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{8} \cdot 13^{4}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(13.62049437\) |
| \(L(\frac12)\) |
\(\approx\) |
\(13.62049437\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 - p T + p^{2} T^{2} )^{2} \) |
| 3 | | \( 1 \) |
| 13 | $C_2^2$ | \( 1 + 35 T + 324 p T^{2} + 35 p^{3} T^{3} + p^{6} T^{4} \) |
| good | 5 | $D_{4}$ | \( ( 1 - 7 T + 208 T^{2} - 7 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 7 | $D_4\times C_2$ | \( 1 - 45 T + 887 T^{2} - 20340 T^{3} + 482820 T^{4} - 20340 p^{3} T^{5} + 887 p^{6} T^{6} - 45 p^{9} T^{7} + p^{12} T^{8} \) |
| 11 | $D_4\times C_2$ | \( 1 - 5 T + 15 T^{2} + 13260 T^{3} - 1804736 T^{4} + 13260 p^{3} T^{5} + 15 p^{6} T^{6} - 5 p^{9} T^{7} + p^{12} T^{8} \) |
| 17 | $D_4\times C_2$ | \( 1 + 130 T + 6321 T^{2} + 97890 T^{3} + 4747972 T^{4} + 97890 p^{3} T^{5} + 6321 p^{6} T^{6} + 130 p^{9} T^{7} + p^{12} T^{8} \) |
| 19 | $D_4\times C_2$ | \( 1 + 3 T - 13657 T^{2} - 156 T^{3} + 139651944 T^{4} - 156 p^{3} T^{5} - 13657 p^{6} T^{6} + 3 p^{9} T^{7} + p^{12} T^{8} \) |
| 23 | $D_4\times C_2$ | \( 1 - 33 T - 23029 T^{2} + 7128 T^{3} + 420392172 T^{4} + 7128 p^{3} T^{5} - 23029 p^{6} T^{6} - 33 p^{9} T^{7} + p^{12} T^{8} \) |
| 29 | $D_4\times C_2$ | \( 1 + 198 T - 11563 T^{2} + 393822 T^{3} + 1026318612 T^{4} + 393822 p^{3} T^{5} - 11563 p^{6} T^{6} + 198 p^{9} T^{7} + p^{12} T^{8} \) |
| 31 | $D_{4}$ | \( ( 1 - 280 T + 47934 T^{2} - 280 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 37 | $D_4\times C_2$ | \( 1 - 702 T + 269165 T^{2} - 85877766 T^{3} + 22486674900 T^{4} - 85877766 p^{3} T^{5} + 269165 p^{6} T^{6} - 702 p^{9} T^{7} + p^{12} T^{8} \) |
| 41 | $D_4\times C_2$ | \( 1 - 242 T - 72219 T^{2} + 1708278 T^{3} + 8317799404 T^{4} + 1708278 p^{3} T^{5} - 72219 p^{6} T^{6} - 242 p^{9} T^{7} + p^{12} T^{8} \) |
| 43 | $D_4\times C_2$ | \( 1 - 93 T - 118621 T^{2} + 2952192 T^{3} + 9188633808 T^{4} + 2952192 p^{3} T^{5} - 118621 p^{6} T^{6} - 93 p^{9} T^{7} + p^{12} T^{8} \) |
| 47 | $D_{4}$ | \( ( 1 + 224 T + 50062 T^{2} + 224 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 53 | $D_{4}$ | \( ( 1 - 535 T + 369256 T^{2} - 535 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 59 | $D_4\times C_2$ | \( 1 + 389 T - 294609 T^{2} + 13681908 T^{3} + 125594875600 T^{4} + 13681908 p^{3} T^{5} - 294609 p^{6} T^{6} + 389 p^{9} T^{7} + p^{12} T^{8} \) |
| 61 | $D_4\times C_2$ | \( 1 + 654 T - 77623 T^{2} + 33600558 T^{3} + 106763725164 T^{4} + 33600558 p^{3} T^{5} - 77623 p^{6} T^{6} + 654 p^{9} T^{7} + p^{12} T^{8} \) |
| 67 | $D_4\times C_2$ | \( 1 - 107 T - 377621 T^{2} + 22732792 T^{3} + 57473647144 T^{4} + 22732792 p^{3} T^{5} - 377621 p^{6} T^{6} - 107 p^{9} T^{7} + p^{12} T^{8} \) |
| 71 | $D_4\times C_2$ | \( 1 + 569 T - 453417 T^{2} + 34911564 T^{3} + 360027736492 T^{4} + 34911564 p^{3} T^{5} - 453417 p^{6} T^{6} + 569 p^{9} T^{7} + p^{12} T^{8} \) |
| 73 | $D_{4}$ | \( ( 1 + 623 T + 11820 p T^{2} + 623 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 79 | $D_{4}$ | \( ( 1 - 760 T + 1005486 T^{2} - 760 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 83 | $D_{4}$ | \( ( 1 - 1764 T + 1851190 T^{2} - 1764 p^{3} T^{3} + p^{6} T^{4} )^{2} \) |
| 89 | $D_4\times C_2$ | \( 1 + 871 T - 788823 T^{2} + 119785146 T^{3} + 1362845153206 T^{4} + 119785146 p^{3} T^{5} - 788823 p^{6} T^{6} + 871 p^{9} T^{7} + p^{12} T^{8} \) |
| 97 | $D_4\times C_2$ | \( 1 - 879 T - 1154671 T^{2} - 89628114 T^{3} + 2176390961022 T^{4} - 89628114 p^{3} T^{5} - 1154671 p^{6} T^{6} - 879 p^{9} T^{7} + p^{12} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.351677722216081575132911588700, −7.964241958668316890015190158306, −7.88599166697136534568745697649, −7.78438425776683786004184099328, −7.36099028925500206586002839055, −7.10354203636991314373746697842, −6.46355077667159471640575672649, −6.38516318401076472011438340165, −6.13997424613525930518424729477, −5.92837688071441818604480452703, −5.52632151494357179259669430862, −5.37799588187169425345616153859, −4.99365613830984625368197838982, −4.52185073179544625738771646494, −4.46249150196210433738294830168, −4.46049190678120679058239898748, −4.05385768611458763682472827342, −3.61021558312856473162615933066, −2.96490903993867392390796676747, −2.47630540752822460522709439477, −2.41165889359856809415857468983, −1.84304207419070282062017992115, −1.84247225630532091582221706074, −0.942456556758303984751659105397, −0.54257916809223912304581213623,
0.54257916809223912304581213623, 0.942456556758303984751659105397, 1.84247225630532091582221706074, 1.84304207419070282062017992115, 2.41165889359856809415857468983, 2.47630540752822460522709439477, 2.96490903993867392390796676747, 3.61021558312856473162615933066, 4.05385768611458763682472827342, 4.46049190678120679058239898748, 4.46249150196210433738294830168, 4.52185073179544625738771646494, 4.99365613830984625368197838982, 5.37799588187169425345616153859, 5.52632151494357179259669430862, 5.92837688071441818604480452703, 6.13997424613525930518424729477, 6.38516318401076472011438340165, 6.46355077667159471640575672649, 7.10354203636991314373746697842, 7.36099028925500206586002839055, 7.78438425776683786004184099328, 7.88599166697136534568745697649, 7.964241958668316890015190158306, 8.351677722216081575132911588700