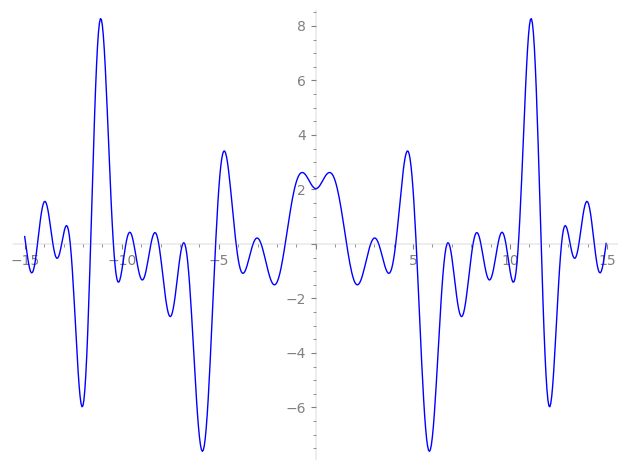
| L(s) = 1 | + 1.90·3-s − 1.17·7-s + 2.61·9-s − 2.23·21-s + 1.17·23-s + 3.07·27-s + 0.618·29-s − 0.618·41-s − 1.90·43-s − 1.90·47-s + 0.381·49-s + 1.61·61-s − 3.07·63-s + 2.23·69-s + 3.23·81-s − 1.17·83-s + 1.17·87-s − 1.61·89-s − 1.61·101-s − 1.90·107-s − 0.618·109-s + ⋯ |
| L(s) = 1 | + 1.90·3-s − 1.17·7-s + 2.61·9-s − 2.23·21-s + 1.17·23-s + 3.07·27-s + 0.618·29-s − 0.618·41-s − 1.90·43-s − 1.90·47-s + 0.381·49-s + 1.61·61-s − 3.07·63-s + 2.23·69-s + 3.23·81-s − 1.17·83-s + 1.17·87-s − 1.61·89-s − 1.61·101-s − 1.90·107-s − 0.618·109-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2000 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2000 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(2.029848752\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.029848752\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 \) |
| 5 | \( 1 \) |
| good | 3 | \( 1 - 1.90T + T^{2} \) |
| 7 | \( 1 + 1.17T + T^{2} \) |
| 11 | \( 1 - T^{2} \) |
| 13 | \( 1 - T^{2} \) |
| 17 | \( 1 - T^{2} \) |
| 19 | \( 1 - T^{2} \) |
| 23 | \( 1 - 1.17T + T^{2} \) |
| 29 | \( 1 - 0.618T + T^{2} \) |
| 31 | \( 1 - T^{2} \) |
| 37 | \( 1 - T^{2} \) |
| 41 | \( 1 + 0.618T + T^{2} \) |
| 43 | \( 1 + 1.90T + T^{2} \) |
| 47 | \( 1 + 1.90T + T^{2} \) |
| 53 | \( 1 - T^{2} \) |
| 59 | \( 1 - T^{2} \) |
| 61 | \( 1 - 1.61T + T^{2} \) |
| 67 | \( 1 + T^{2} \) |
| 71 | \( 1 - T^{2} \) |
| 73 | \( 1 - T^{2} \) |
| 79 | \( 1 - T^{2} \) |
| 83 | \( 1 + 1.17T + T^{2} \) |
| 89 | \( 1 + 1.61T + T^{2} \) |
| 97 | \( 1 - T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.378034101247281227791448576187, −8.497721086081676190040414239515, −8.094325744257204351811132448365, −6.86081828250606426702463543609, −6.75284409022418682926607957631, −5.16548764909187145838187342935, −4.11034849252736419619728092856, −3.23547013286212241593639152428, −2.82116663127156632596090079235, −1.58189053719270314179509749706,
1.58189053719270314179509749706, 2.82116663127156632596090079235, 3.23547013286212241593639152428, 4.11034849252736419619728092856, 5.16548764909187145838187342935, 6.75284409022418682926607957631, 6.86081828250606426702463543609, 8.094325744257204351811132448365, 8.497721086081676190040414239515, 9.378034101247281227791448576187