| L(s) = 1 | + (0.120 + 0.992i)2-s + (0.592 − 1.56i)3-s + (−0.970 + 0.239i)4-s + (1.43 + 0.754i)5-s + (1.62 + 0.399i)6-s + (1.16 − 3.06i)7-s + (−0.354 − 0.935i)8-s + (0.158 + 0.140i)9-s + (−0.575 + 1.51i)10-s + (−4.50 + 2.36i)11-s + (−0.201 + 1.65i)12-s + (5.00 − 1.23i)13-s + (3.18 + 0.785i)14-s + (2.03 − 1.79i)15-s + (0.885 − 0.464i)16-s + (2.77 − 0.684i)17-s + ⋯ |
| L(s) = 1 | + (0.0852 + 0.701i)2-s + (0.341 − 0.901i)3-s + (−0.485 + 0.119i)4-s + (0.643 + 0.337i)5-s + (0.661 + 0.163i)6-s + (0.439 − 1.16i)7-s + (−0.125 − 0.330i)8-s + (0.0528 + 0.0467i)9-s + (−0.182 + 0.480i)10-s + (−1.35 + 0.713i)11-s + (−0.0581 + 0.478i)12-s + (1.38 − 0.342i)13-s + (0.851 + 0.209i)14-s + (0.524 − 0.464i)15-s + (0.221 − 0.116i)16-s + (0.673 − 0.165i)17-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 158 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.994 - 0.102i)\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 158 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.994 - 0.102i)\, \overline{\Lambda}(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.36483 + 0.0700811i\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.36483 + 0.0700811i\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 + (-0.120 - 0.992i)T \) |
| 79 | \( 1 + (-6.89 - 5.61i)T \) |
| good | 3 | \( 1 + (-0.592 + 1.56i)T + (-2.24 - 1.98i)T^{2} \) |
| 5 | \( 1 + (-1.43 - 0.754i)T + (2.84 + 4.11i)T^{2} \) |
| 7 | \( 1 + (-1.16 + 3.06i)T + (-5.23 - 4.64i)T^{2} \) |
| 11 | \( 1 + (4.50 - 2.36i)T + (6.24 - 9.05i)T^{2} \) |
| 13 | \( 1 + (-5.00 + 1.23i)T + (11.5 - 6.04i)T^{2} \) |
| 17 | \( 1 + (-2.77 + 0.684i)T + (15.0 - 7.90i)T^{2} \) |
| 19 | \( 1 + (4.40 - 6.38i)T + (-6.73 - 17.7i)T^{2} \) |
| 23 | \( 1 + 7.48T + 23T^{2} \) |
| 29 | \( 1 + (4.74 - 4.20i)T + (3.49 - 28.7i)T^{2} \) |
| 31 | \( 1 + (0.247 + 2.03i)T + (-30.0 + 7.41i)T^{2} \) |
| 37 | \( 1 + (1.64 - 2.38i)T + (-13.1 - 34.5i)T^{2} \) |
| 41 | \( 1 + (5.04 + 2.64i)T + (23.2 + 33.7i)T^{2} \) |
| 43 | \( 1 + (4.03 + 2.11i)T + (24.4 + 35.3i)T^{2} \) |
| 47 | \( 1 + (-2.26 - 3.28i)T + (-16.6 + 43.9i)T^{2} \) |
| 53 | \( 1 + (-1.47 - 3.89i)T + (-39.6 + 35.1i)T^{2} \) |
| 59 | \( 1 + (-7.26 - 1.79i)T + (52.2 + 27.4i)T^{2} \) |
| 61 | \( 1 + (-5.10 + 7.39i)T + (-21.6 - 57.0i)T^{2} \) |
| 67 | \( 1 + (-0.628 + 5.17i)T + (-65.0 - 16.0i)T^{2} \) |
| 71 | \( 1 + (-3.80 - 10.0i)T + (-53.1 + 47.0i)T^{2} \) |
| 73 | \( 1 + (6.89 + 1.69i)T + (64.6 + 33.9i)T^{2} \) |
| 83 | \( 1 + (-13.2 + 3.26i)T + (73.4 - 38.5i)T^{2} \) |
| 89 | \( 1 + (0.560 - 1.47i)T + (-66.6 - 59.0i)T^{2} \) |
| 97 | \( 1 + (1.77 - 2.56i)T + (-34.3 - 90.6i)T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
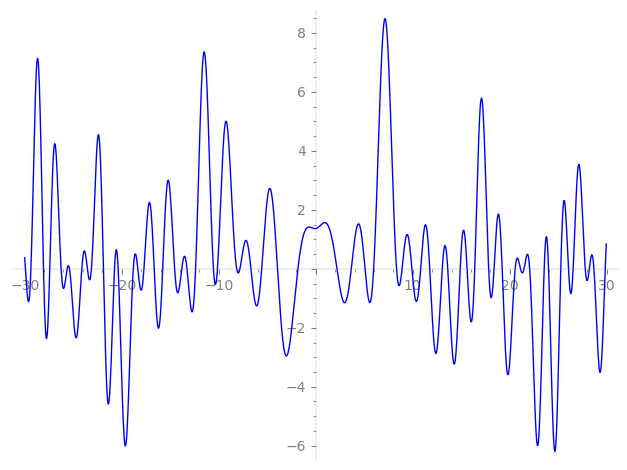
Imaginary part of the first few zeros on the critical line
−13.26869003897689454691638349501, −12.38486399328763918955503894194, −10.54177292288431372661590626915, −10.13113960859691302282064698175, −8.147727214330793157874027801035, −7.81503433890839095834035194361, −6.67818714991712830022472158845, −5.56976158914754967368288728288, −3.93919796297097070791212095214, −1.83805078354078986151444170432,
2.19135503484759461525808205285, 3.66605329499382411390625010381, 5.08382737223435757958763806143, 5.97052806977474441648997168730, 8.333159981325188168310707871009, 8.901891993897954218885584936006, 9.913932631250593884211087039887, 10.81409530375107077066590969500, 11.75318664634821665020448105551, 13.04127672430269215641507524591