↑

Properties

Label 8-1488e4-1.1-c0e4-0-3
Degree $8$
Conductor $4.902\times 10^{12}$
Sign $1$
Analytic cond. $0.304116$
Root an. cond. $0.861747$
Motivic weight $0$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 3-s + 2·7-s − 2·13-s + 2·19-s + 2·21-s + 4·25-s + 31-s − 2·37-s − 2·39-s − 3·43-s + 49-s + 2·57-s − 2·61-s + 2·67-s − 2·73-s + 4·75-s − 3·79-s − 4·91-s + 93-s + 3·97-s − 3·103-s + 3·109-s − 2·111-s − 121-s + 127-s − 3·129-s + 131-s + ⋯
L(s)  = 1  + 3-s + 2·7-s − 2·13-s + 2·19-s + 2·21-s + 4·25-s + 31-s − 2·37-s − 2·39-s − 3·43-s + 49-s + 2·57-s − 2·61-s + 2·67-s − 2·73-s + 4·75-s − 3·79-s − 4·91-s + 93-s + 3·97-s − 3·103-s + 3·109-s − 2·111-s − 121-s + 127-s − 3·129-s + 131-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{16} \cdot 3^{4} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]

Invariants

Degree: \(8\)
Conductor: \(2^{16} \cdot 3^{4} \cdot 31^{4}\)
Sign: $1$
Analytic conductor: \(0.304116\)
Root analytic conductor: \(0.861747\)
Motivic weight: \(0\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((8,\ 2^{16} \cdot 3^{4} \cdot 31^{4} ,\ ( \ : 0, 0, 0, 0 ),\ 1 )\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(2.096968048\)
\(L(\frac12)\) \(\approx\) \(2.096968048\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad2 \( 1 \)
3$C_4$ \( 1 - T + T^{2} - T^{3} + T^{4} \)
31$C_4$ \( 1 - T + T^{2} - T^{3} + T^{4} \)
good5$C_1$$\times$$C_1$ \( ( 1 - T )^{4}( 1 + T )^{4} \)
7$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )^{2} \)
11$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
13$C_4$ \( ( 1 + T + T^{2} + T^{3} + T^{4} )^{2} \)
17$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
19$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )^{2} \)
23$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
29$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
37$C_4$ \( ( 1 + T + T^{2} + T^{3} + T^{4} )^{2} \)
41$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
43$C_1$$\times$$C_4$ \( ( 1 + T )^{4}( 1 - T + T^{2} - T^{3} + T^{4} ) \)
47$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
53$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
59$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
61$C_4$ \( ( 1 + T + T^{2} + T^{3} + T^{4} )^{2} \)
67$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )^{2} \)
71$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
73$C_4$ \( ( 1 + T + T^{2} + T^{3} + T^{4} )^{2} \)
79$C_1$$\times$$C_4$ \( ( 1 + T )^{4}( 1 - T + T^{2} - T^{3} + T^{4} ) \)
83$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
89$C_4$$\times$$C_4$ \( ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} ) \)
97$C_1$$\times$$C_4$ \( ( 1 - T )^{4}( 1 + T + T^{2} + T^{3} + T^{4} ) \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

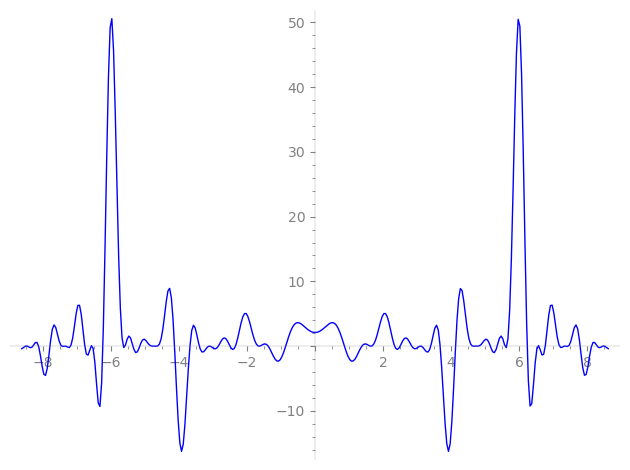
Imaginary part of the first few zeros on the critical line

−7.18856313291789662917199479182, −6.77065082541891905727893728622, −6.58499904408377229189990961170, −6.54684092144748555003067577882, −6.24021788325768331491370272607, −5.64280647091914395174196937958, −5.58542848718481292594954629898, −5.35543497518795593964392871687, −5.15462758307147226714010521129, −4.78975823983381052812114442522, −4.74039603216732057396849673626, −4.73765139584929595257139838069, −4.63565855609123401904022458158, −4.13372314885701424871666850504, −3.67843462891121149306594932282, −3.40315464620159521524429660193, −3.11587770871967752236824471454, −3.09242329769796765660355549813, −2.84318413770895777631909381435, −2.50354207201746235452166729523, −2.34015641020157063965635407893, −1.66627838901613839352309436874, −1.62079118385713443483666287723, −1.37873456310526249170272451904, −0.863297079943386994698842623741, 0.863297079943386994698842623741, 1.37873456310526249170272451904, 1.62079118385713443483666287723, 1.66627838901613839352309436874, 2.34015641020157063965635407893, 2.50354207201746235452166729523, 2.84318413770895777631909381435, 3.09242329769796765660355549813, 3.11587770871967752236824471454, 3.40315464620159521524429660193, 3.67843462891121149306594932282, 4.13372314885701424871666850504, 4.63565855609123401904022458158, 4.73765139584929595257139838069, 4.74039603216732057396849673626, 4.78975823983381052812114442522, 5.15462758307147226714010521129, 5.35543497518795593964392871687, 5.58542848718481292594954629898, 5.64280647091914395174196937958, 6.24021788325768331491370272607, 6.54684092144748555003067577882, 6.58499904408377229189990961170, 6.77065082541891905727893728622, 7.18856313291789662917199479182

Graph of the $Z$-function along the critical line