↑

Properties

Label 4-1476e2-1.1-c0e2-0-0
Degree $4$
Conductor $2178576$
Sign $1$
Analytic cond. $0.542608$
Root an. cond. $0.858265$
Motivic weight $0$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

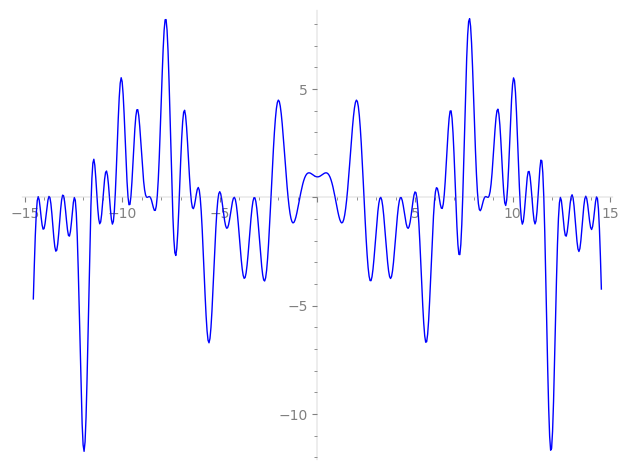
L(s)  = 1  − 4-s + 2·13-s + 16-s − 2·17-s + 2·25-s + 2·29-s − 2·52-s − 2·53-s − 64-s + 2·68-s − 2·89-s − 2·97-s − 2·100-s + 2·101-s + 2·109-s + 4·113-s − 2·116-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 2·169-s + ⋯
L(s)  = 1  − 4-s + 2·13-s + 16-s − 2·17-s + 2·25-s + 2·29-s − 2·52-s − 2·53-s − 64-s + 2·68-s − 2·89-s − 2·97-s − 2·100-s + 2·101-s + 2·109-s + 4·113-s − 2·116-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 2·169-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2178576 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2178576 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(2178576\)    =    \(2^{4} \cdot 3^{4} \cdot 41^{2}\)
Sign: $1$
Analytic conductor: \(0.542608\)
Root analytic conductor: \(0.858265\)
Motivic weight: \(0\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 2178576,\ (\ :0, 0),\ 1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.9473887272\)
\(L(\frac12)\) \(\approx\) \(0.9473887272\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad2$C_2$ \( 1 + T^{2} \)
3 \( 1 \)
41$C_2$ \( 1 + T^{2} \)
good5$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
7$C_2^2$ \( 1 + T^{4} \)
11$C_2^2$ \( 1 + T^{4} \)
13$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
17$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
19$C_2^2$ \( 1 + T^{4} \)
23$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
29$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
31$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
37$C_2$ \( ( 1 + T^{2} )^{2} \)
43$C_2$ \( ( 1 + T^{2} )^{2} \)
47$C_2^2$ \( 1 + T^{4} \)
53$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
59$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
61$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
67$C_2^2$ \( 1 + T^{4} \)
71$C_2^2$ \( 1 + T^{4} \)
73$C_2$ \( ( 1 + T^{2} )^{2} \)
79$C_2^2$ \( 1 + T^{4} \)
83$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
89$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
97$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−9.704831876122060835371444793092, −9.561890430294411418112794883507, −8.737664196561247979120011611598, −8.715823320353645584493344671347, −8.559151727886689284541110828795, −8.213029007037247664329148009486, −7.44004441509837131394055170071, −7.08090017972803214860230900017, −6.48142480957307620017995638702, −6.23370285079742484402071226071, −6.00970196310336102970396509136, −5.08901483010617672216160921962, −4.92137836961349848867725136209, −4.28366222529984905136063354079, −4.24999549860589339618006629746, −3.24669359978630547319164930563, −3.21860103441869062304470821958, −2.38320885102768394452383890357, −1.50623696277586610907880921491, −0.902508982075131815535097570607, 0.902508982075131815535097570607, 1.50623696277586610907880921491, 2.38320885102768394452383890357, 3.21860103441869062304470821958, 3.24669359978630547319164930563, 4.24999549860589339618006629746, 4.28366222529984905136063354079, 4.92137836961349848867725136209, 5.08901483010617672216160921962, 6.00970196310336102970396509136, 6.23370285079742484402071226071, 6.48142480957307620017995638702, 7.08090017972803214860230900017, 7.44004441509837131394055170071, 8.213029007037247664329148009486, 8.559151727886689284541110828795, 8.715823320353645584493344671347, 8.737664196561247979120011611598, 9.561890430294411418112794883507, 9.704831876122060835371444793092

Graph of the $Z$-function along the critical line