| L(s) = 1 | − 2·2-s − 5·4-s + 8·5-s + 20·8-s − 16·10-s + 5·16-s + 46·17-s + 28·19-s − 40·20-s − 14·23-s + 39·25-s − 50·31-s − 118·32-s − 92·34-s − 56·38-s + 160·40-s + 28·46-s − 98·47-s + 62·49-s − 78·50-s + 28·53-s + 88·61-s + 100·62-s + 111·64-s − 230·68-s − 140·76-s − 74·79-s + ⋯ |
| L(s) = 1 | − 2-s − 5/4·4-s + 8/5·5-s + 5/2·8-s − 8/5·10-s + 5/16·16-s + 2.70·17-s + 1.47·19-s − 2·20-s − 0.608·23-s + 1.55·25-s − 1.61·31-s − 3.68·32-s − 2.70·34-s − 1.47·38-s + 4·40-s + 0.608·46-s − 2.08·47-s + 1.26·49-s − 1.55·50-s + 0.528·53-s + 1.44·61-s + 1.61·62-s + 1.73·64-s − 3.38·68-s − 1.84·76-s − 0.936·79-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 18225 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(3-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 18225 ^{s/2} \, \Gamma_{\C}(s+1)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{3}{2})\) |
\(\approx\) |
\(1.071012326\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.071012326\) |
| \(L(2)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 3 | | \( 1 \) |
| 5 | $C_2$ | \( 1 - 8 T + p^{2} T^{2} \) |
| good | 2 | $C_2$ | \( ( 1 + T + p^{2} T^{2} )^{2} \) |
| 7 | $C_2^2$ | \( 1 - 62 T^{2} + p^{4} T^{4} \) |
| 11 | $C_2^2$ | \( 1 + 199 T^{2} + p^{4} T^{4} \) |
| 13 | $C_2^2$ | \( 1 - 113 T^{2} + p^{4} T^{4} \) |
| 17 | $C_2$ | \( ( 1 - 23 T + p^{2} T^{2} )^{2} \) |
| 19 | $C_2$ | \( ( 1 - 14 T + p^{2} T^{2} )^{2} \) |
| 23 | $C_2$ | \( ( 1 + 7 T + p^{2} T^{2} )^{2} \) |
| 29 | $C_2^2$ | \( 1 - 1673 T^{2} + p^{4} T^{4} \) |
| 31 | $C_2$ | \( ( 1 + 25 T + p^{2} T^{2} )^{2} \) |
| 37 | $C_2^2$ | \( 1 + 178 T^{2} + p^{4} T^{4} \) |
| 41 | $C_2^2$ | \( 1 - 2786 T^{2} + p^{4} T^{4} \) |
| 43 | $C_2^2$ | \( 1 - 3473 T^{2} + p^{4} T^{4} \) |
| 47 | $C_2$ | \( ( 1 + 49 T + p^{2} T^{2} )^{2} \) |
| 53 | $C_2$ | \( ( 1 - 14 T + p^{2} T^{2} )^{2} \) |
| 59 | $C_2^2$ | \( 1 - 6062 T^{2} + p^{4} T^{4} \) |
| 61 | $C_2$ | \( ( 1 - 44 T + p^{2} T^{2} )^{2} \) |
| 67 | $C_2^2$ | \( 1 - 4622 T^{2} + p^{4} T^{4} \) |
| 71 | $C_2^2$ | \( 1 - 9758 T^{2} + p^{4} T^{4} \) |
| 73 | $C_1$$\times$$C_1$ | \( ( 1 - p T )^{2}( 1 + p T )^{2} \) |
| 79 | $C_2$ | \( ( 1 + 37 T + p^{2} T^{2} )^{2} \) |
| 83 | $C_2$ | \( ( 1 - 116 T + p^{2} T^{2} )^{2} \) |
| 89 | $C_2^2$ | \( 1 + 34 T^{2} + p^{4} T^{4} \) |
| 97 | $C_2^2$ | \( 1 - 12734 T^{2} + p^{4} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
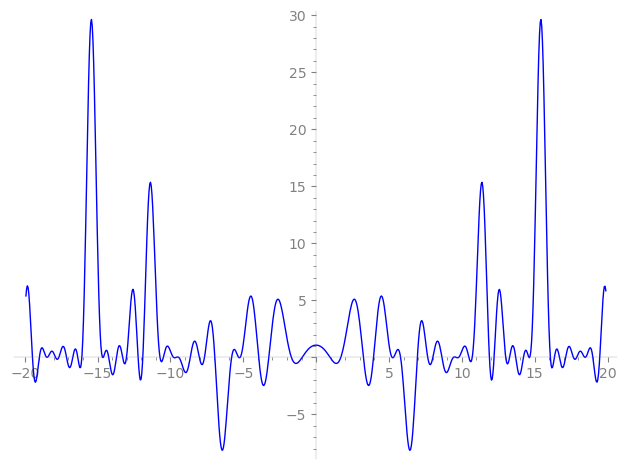
Imaginary part of the first few zeros on the critical line
−13.27739047222339600482843778846, −13.01311446509182224511424580094, −12.21554048307745055700078555112, −11.89440559418743414493472113596, −10.71458093163368727443007528288, −10.48462576661018914831656225985, −9.783677443690611734661349983754, −9.599611856034358848112237736932, −9.431015022389270099359299302336, −8.636250793607475271511693499619, −8.013596345370321694350786965021, −7.66124022858928342547117465445, −6.94852542338980132184220431283, −5.79744115943471452123934807274, −5.31425940147799744845997758749, −5.21154962727406307687574987004, −3.94081590981531766672814753063, −3.24669887644390412664694550518, −1.69575349913410456652536905450, −0.954468687239003510964642111994,
0.954468687239003510964642111994, 1.69575349913410456652536905450, 3.24669887644390412664694550518, 3.94081590981531766672814753063, 5.21154962727406307687574987004, 5.31425940147799744845997758749, 5.79744115943471452123934807274, 6.94852542338980132184220431283, 7.66124022858928342547117465445, 8.013596345370321694350786965021, 8.636250793607475271511693499619, 9.431015022389270099359299302336, 9.599611856034358848112237736932, 9.783677443690611734661349983754, 10.48462576661018914831656225985, 10.71458093163368727443007528288, 11.89440559418743414493472113596, 12.21554048307745055700078555112, 13.01311446509182224511424580094, 13.27739047222339600482843778846