| L(s) = 1 | + 2·5-s + 32·7-s − 58·11-s + 66·13-s + 68·17-s + 154·19-s − 126·23-s − 197·25-s − 136·29-s + 264·31-s + 64·35-s + 492·37-s − 298·41-s + 574·43-s + 48·47-s + 256·49-s − 132·53-s − 116·55-s + 748·59-s + 752·61-s + 132·65-s + 400·67-s + 844·71-s + 2.23e3·73-s − 1.85e3·77-s − 376·79-s − 40·83-s + ⋯ |
| L(s) = 1 | + 0.178·5-s + 1.72·7-s − 1.58·11-s + 1.40·13-s + 0.970·17-s + 1.85·19-s − 1.14·23-s − 1.57·25-s − 0.870·29-s + 1.52·31-s + 0.309·35-s + 2.18·37-s − 1.13·41-s + 2.03·43-s + 0.148·47-s + 0.746·49-s − 0.342·53-s − 0.284·55-s + 1.65·59-s + 1.57·61-s + 0.251·65-s + 0.729·67-s + 1.41·71-s + 3.58·73-s − 2.74·77-s − 0.535·79-s − 0.0528·83-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{8} \cdot 17^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(4-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{8} \cdot 17^{4}\right)^{s/2} \, \Gamma_{\C}(s+3/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(2)\) |
\(\approx\) |
\(15.68332447\) |
| \(L(\frac12)\) |
\(\approx\) |
\(15.68332447\) |
| \(L(\frac{5}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 3 | | \( 1 \) |
| 17 | $C_1$ | \( ( 1 - p T )^{4} \) |
| good | 5 | $C_2 \wr S_4$ | \( 1 - 2 T + 201 T^{2} - 498 T^{3} + 19768 T^{4} - 498 p^{3} T^{5} + 201 p^{6} T^{6} - 2 p^{9} T^{7} + p^{12} T^{8} \) |
| 7 | $C_2 \wr S_4$ | \( 1 - 32 T + 768 T^{2} - 14640 T^{3} + 248350 T^{4} - 14640 p^{3} T^{5} + 768 p^{6} T^{6} - 32 p^{9} T^{7} + p^{12} T^{8} \) |
| 11 | $C_2 \wr S_4$ | \( 1 + 58 T + 1713 T^{2} - 21414 T^{3} - 218340 p T^{4} - 21414 p^{3} T^{5} + 1713 p^{6} T^{6} + 58 p^{9} T^{7} + p^{12} T^{8} \) |
| 13 | $C_2 \wr S_4$ | \( 1 - 66 T + 4073 T^{2} - 186882 T^{3} + 6678908 T^{4} - 186882 p^{3} T^{5} + 4073 p^{6} T^{6} - 66 p^{9} T^{7} + p^{12} T^{8} \) |
| 19 | $C_2 \wr S_4$ | \( 1 - 154 T + 20453 T^{2} - 1632858 T^{3} + 145227820 T^{4} - 1632858 p^{3} T^{5} + 20453 p^{6} T^{6} - 154 p^{9} T^{7} + p^{12} T^{8} \) |
| 23 | $C_2 \wr S_4$ | \( 1 + 126 T + 33061 T^{2} + 2599210 T^{3} + 463573912 T^{4} + 2599210 p^{3} T^{5} + 33061 p^{6} T^{6} + 126 p^{9} T^{7} + p^{12} T^{8} \) |
| 29 | $C_2 \wr S_4$ | \( 1 + 136 T + 76488 T^{2} + 10216296 T^{3} + 2551909534 T^{4} + 10216296 p^{3} T^{5} + 76488 p^{6} T^{6} + 136 p^{9} T^{7} + p^{12} T^{8} \) |
| 31 | $C_2 \wr S_4$ | \( 1 - 264 T + 129348 T^{2} - 21787592 T^{3} + 5819583174 T^{4} - 21787592 p^{3} T^{5} + 129348 p^{6} T^{6} - 264 p^{9} T^{7} + p^{12} T^{8} \) |
| 37 | $C_2 \wr S_4$ | \( 1 - 492 T + 211140 T^{2} - 57883252 T^{3} + 15094834902 T^{4} - 57883252 p^{3} T^{5} + 211140 p^{6} T^{6} - 492 p^{9} T^{7} + p^{12} T^{8} \) |
| 41 | $C_2 \wr S_4$ | \( 1 + 298 T + 235629 T^{2} + 56299506 T^{3} + 23008885660 T^{4} + 56299506 p^{3} T^{5} + 235629 p^{6} T^{6} + 298 p^{9} T^{7} + p^{12} T^{8} \) |
| 43 | $C_2 \wr S_4$ | \( 1 - 574 T + 358773 T^{2} - 123885478 T^{3} + 44465832668 T^{4} - 123885478 p^{3} T^{5} + 358773 p^{6} T^{6} - 574 p^{9} T^{7} + p^{12} T^{8} \) |
| 47 | $C_2 \wr S_4$ | \( 1 - 48 T + 179560 T^{2} + 7256560 T^{3} + 23683181614 T^{4} + 7256560 p^{3} T^{5} + 179560 p^{6} T^{6} - 48 p^{9} T^{7} + p^{12} T^{8} \) |
| 53 | $C_2 \wr S_4$ | \( 1 + 132 T + 34164 T^{2} + 50123340 T^{3} + 31093211366 T^{4} + 50123340 p^{3} T^{5} + 34164 p^{6} T^{6} + 132 p^{9} T^{7} + p^{12} T^{8} \) |
| 59 | $C_2 \wr S_4$ | \( 1 - 748 T + 655936 T^{2} - 308842956 T^{3} + 182376597806 T^{4} - 308842956 p^{3} T^{5} + 655936 p^{6} T^{6} - 748 p^{9} T^{7} + p^{12} T^{8} \) |
| 61 | $C_2 \wr S_4$ | \( 1 - 752 T + 513876 T^{2} - 82872912 T^{3} + 44244131734 T^{4} - 82872912 p^{3} T^{5} + 513876 p^{6} T^{6} - 752 p^{9} T^{7} + p^{12} T^{8} \) |
| 67 | $C_2 \wr S_4$ | \( 1 - 400 T + 1158860 T^{2} - 354591120 T^{3} + 516548758358 T^{4} - 354591120 p^{3} T^{5} + 1158860 p^{6} T^{6} - 400 p^{9} T^{7} + p^{12} T^{8} \) |
| 71 | $C_2 \wr S_4$ | \( 1 - 844 T + 1421008 T^{2} - 820644348 T^{3} + 750055995134 T^{4} - 820644348 p^{3} T^{5} + 1421008 p^{6} T^{6} - 844 p^{9} T^{7} + p^{12} T^{8} \) |
| 73 | $C_2 \wr S_4$ | \( 1 - 2236 T + 3012612 T^{2} - 2845891300 T^{3} + 2052111103190 T^{4} - 2845891300 p^{3} T^{5} + 3012612 p^{6} T^{6} - 2236 p^{9} T^{7} + p^{12} T^{8} \) |
| 79 | $C_2 \wr S_4$ | \( 1 + 376 T + 1232212 T^{2} + 579968248 T^{3} + 754413387430 T^{4} + 579968248 p^{3} T^{5} + 1232212 p^{6} T^{6} + 376 p^{9} T^{7} + p^{12} T^{8} \) |
| 83 | $C_2 \wr S_4$ | \( 1 + 40 T + 1665400 T^{2} - 159332120 T^{3} + 1228987348638 T^{4} - 159332120 p^{3} T^{5} + 1665400 p^{6} T^{6} + 40 p^{9} T^{7} + p^{12} T^{8} \) |
| 89 | $C_2 \wr S_4$ | \( 1 + 1312 T + 2913736 T^{2} + 2538466288 T^{3} + 3129297837486 T^{4} + 2538466288 p^{3} T^{5} + 2913736 p^{6} T^{6} + 1312 p^{9} T^{7} + p^{12} T^{8} \) |
| 97 | $C_2 \wr S_4$ | \( 1 - 2272 T + 2568728 T^{2} - 12704208 p T^{3} + 459626740718 T^{4} - 12704208 p^{4} T^{5} + 2568728 p^{6} T^{6} - 2272 p^{9} T^{7} + p^{12} T^{8} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
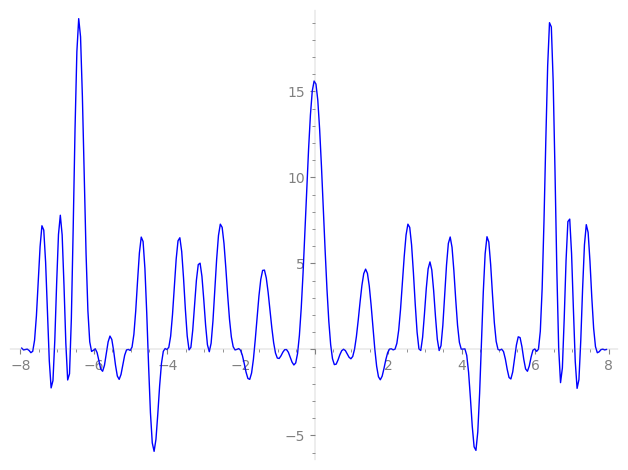
Imaginary part of the first few zeros on the critical line
−6.63660740267315489689161680480, −6.08508949337430586918497492492, −5.99733478884331666398602856780, −5.94706042939182093079200191998, −5.64726837011355418935282488709, −5.46914314680838672201360191302, −5.10100194964028473977165865777, −5.06606454677296509079904649680, −4.98499000721343510800774043067, −4.52951000816747649322590681768, −4.09508413162966646362410500566, −4.02430939243032256603284855004, −3.99230756798406527590651579502, −3.41761063094689663847149837644, −3.37537946109748421363958309299, −2.89357754337288484563553165578, −2.83883584924469473677241778549, −2.18164787124484314017565078300, −2.11306127646237486157867132118, −2.02857154537350431373408638069, −1.63726613737106357208832861462, −1.08466898684855709779400771400, −0.802607495575215146708534690726, −0.77095324102998860857668655906, −0.44984014277871671272391473547,
0.44984014277871671272391473547, 0.77095324102998860857668655906, 0.802607495575215146708534690726, 1.08466898684855709779400771400, 1.63726613737106357208832861462, 2.02857154537350431373408638069, 2.11306127646237486157867132118, 2.18164787124484314017565078300, 2.83883584924469473677241778549, 2.89357754337288484563553165578, 3.37537946109748421363958309299, 3.41761063094689663847149837644, 3.99230756798406527590651579502, 4.02430939243032256603284855004, 4.09508413162966646362410500566, 4.52951000816747649322590681768, 4.98499000721343510800774043067, 5.06606454677296509079904649680, 5.10100194964028473977165865777, 5.46914314680838672201360191302, 5.64726837011355418935282488709, 5.94706042939182093079200191998, 5.99733478884331666398602856780, 6.08508949337430586918497492492, 6.63660740267315489689161680480