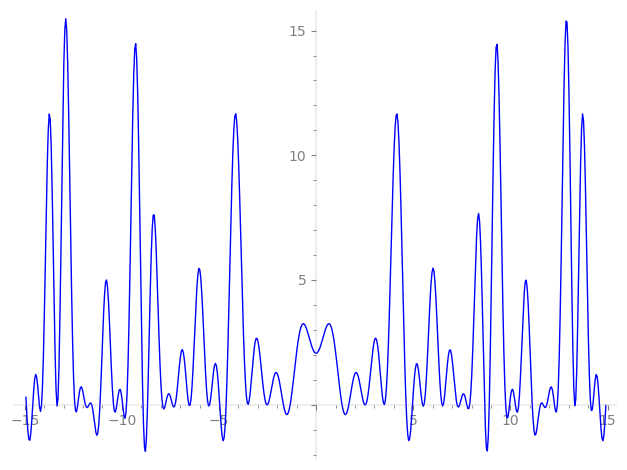
| L(s) = 1 | + 2·4-s + 7-s − 2·13-s + 3·16-s + 2·19-s − 25-s + 2·28-s + 31-s − 2·37-s − 2·43-s + 49-s − 4·52-s + 61-s + 4·64-s − 2·67-s + 73-s + 4·76-s − 2·79-s − 2·91-s + 4·97-s − 2·100-s + 103-s − 2·109-s + 3·112-s − 121-s + 2·124-s + 127-s + ⋯ |
| L(s) = 1 | + 2·4-s + 7-s − 2·13-s + 3·16-s + 2·19-s − 25-s + 2·28-s + 31-s − 2·37-s − 2·43-s + 49-s − 4·52-s + 61-s + 4·64-s − 2·67-s + 73-s + 4·76-s − 2·79-s − 2·91-s + 4·97-s − 2·100-s + 103-s − 2·109-s + 3·112-s − 121-s + 2·124-s + 127-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2368521 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2368521 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(2.062845736\) |
| \(L(\frac12)\) |
\(\approx\) |
\(2.062845736\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 3 | | \( 1 \) |
| 19 | $C_1$ | \( ( 1 - T )^{2} \) |
| good | 2 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 5 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 7 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{2}( 1 + T + T^{2} ) \) |
| 11 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 13 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 17 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 23 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{2}( 1 + T )^{2} \) |
| 29 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 31 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{2}( 1 + T + T^{2} ) \) |
| 37 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 41 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 43 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 47 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 53 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 59 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 61 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{2}( 1 + T + T^{2} ) \) |
| 67 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 71 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 73 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{2}( 1 + T + T^{2} ) \) |
| 79 | $C_2$ | \( ( 1 + T + T^{2} )^{2} \) |
| 83 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 89 | $C_2$ | \( ( 1 - T + T^{2} )( 1 + T + T^{2} ) \) |
| 97 | $C_1$ | \( ( 1 - T )^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.957234692703789338578407344723, −9.756974307907275416324768914426, −8.911818576233452463272809483768, −8.676376175225585669733257482283, −7.906277925318936395148503235966, −7.75709023521877443322407063983, −7.39170794713973624650260959775, −7.25727411380110451526731399073, −6.54878749917281417990758012606, −6.47987503532712501661389572456, −5.55592948597905320287143075294, −5.47842805358497058530141016389, −4.96197525067685487367701666691, −4.63151513257975307605923674579, −3.50818336541310667620523576584, −3.50210846922613935971651846994, −2.55077014801167025377895925272, −2.49616759794252448577206942042, −1.68354271794708447845707629030, −1.33439010228231421956922834015,
1.33439010228231421956922834015, 1.68354271794708447845707629030, 2.49616759794252448577206942042, 2.55077014801167025377895925272, 3.50210846922613935971651846994, 3.50818336541310667620523576584, 4.63151513257975307605923674579, 4.96197525067685487367701666691, 5.47842805358497058530141016389, 5.55592948597905320287143075294, 6.47987503532712501661389572456, 6.54878749917281417990758012606, 7.25727411380110451526731399073, 7.39170794713973624650260959775, 7.75709023521877443322407063983, 7.906277925318936395148503235966, 8.676376175225585669733257482283, 8.911818576233452463272809483768, 9.756974307907275416324768914426, 9.957234692703789338578407344723