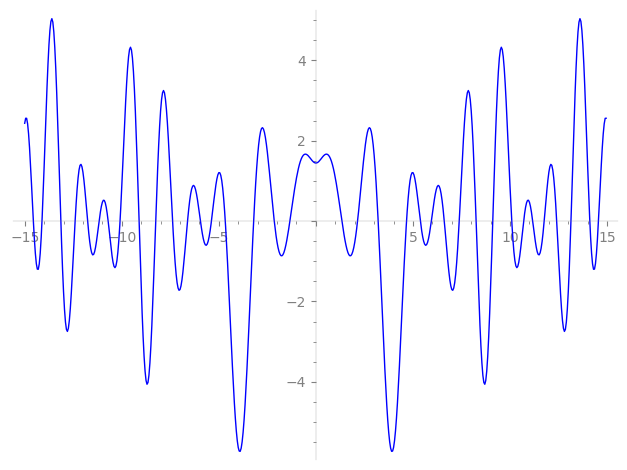
| L(s) = 1 | − 3-s + 4-s + 5-s + 7-s − 12-s − 15-s + 16-s + 20-s − 21-s + 25-s + 27-s + 28-s − 31-s + 35-s − 43-s − 48-s + 49-s − 53-s − 59-s − 60-s + 64-s − 71-s + 73-s − 75-s − 79-s + 80-s − 81-s + ⋯ |
| L(s) = 1 | − 3-s + 4-s + 5-s + 7-s − 12-s − 15-s + 16-s + 20-s − 21-s + 25-s + 27-s + 28-s − 31-s + 35-s − 43-s − 48-s + 49-s − 53-s − 59-s − 60-s + 64-s − 71-s + 73-s − 75-s − 79-s + 80-s − 81-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2555 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2555 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(1.444508201\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.444508201\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 5 | \( 1 - T \) |
| 7 | \( 1 - T \) |
| 73 | \( 1 - T \) |
| good | 2 | \( ( 1 - T )( 1 + T ) \) |
| 3 | \( 1 + T + T^{2} \) |
| 11 | \( ( 1 - T )( 1 + T ) \) |
| 13 | \( ( 1 - T )( 1 + T ) \) |
| 17 | \( ( 1 - T )( 1 + T ) \) |
| 19 | \( ( 1 - T )( 1 + T ) \) |
| 23 | \( ( 1 - T )( 1 + T ) \) |
| 29 | \( ( 1 - T )( 1 + T ) \) |
| 31 | \( 1 + T + T^{2} \) |
| 37 | \( ( 1 - T )( 1 + T ) \) |
| 41 | \( ( 1 - T )( 1 + T ) \) |
| 43 | \( 1 + T + T^{2} \) |
| 47 | \( ( 1 - T )( 1 + T ) \) |
| 53 | \( 1 + T + T^{2} \) |
| 59 | \( 1 + T + T^{2} \) |
| 61 | \( ( 1 - T )( 1 + T ) \) |
| 67 | \( ( 1 - T )( 1 + T ) \) |
| 71 | \( 1 + T + T^{2} \) |
| 79 | \( 1 + T + T^{2} \) |
| 83 | \( ( 1 - T )( 1 + T ) \) |
| 89 | \( ( 1 - T )( 1 + T ) \) |
| 97 | \( ( 1 - T )^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−9.108908833758165671219719608208, −8.251523515270737789507406997438, −7.38220353980112748668537834994, −6.61204612696609718192525077234, −5.94662144115643546774970353250, −5.38129309942741341083262254361, −4.66849580252795647621625332346, −3.20706408374643125181813565258, −2.14529746446223228689409451342, −1.33988953506862944450549930077,
1.33988953506862944450549930077, 2.14529746446223228689409451342, 3.20706408374643125181813565258, 4.66849580252795647621625332346, 5.38129309942741341083262254361, 5.94662144115643546774970353250, 6.61204612696609718192525077234, 7.38220353980112748668537834994, 8.251523515270737789507406997438, 9.108908833758165671219719608208