↑

Properties

Label 1-2527-2527.31-r0-0-0
Degree $1$
Conductor $2527$
Sign $-0.994 - 0.104i$
Analytic cond. $11.7353$
Root an. cond. $11.7353$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.191 + 0.981i)2-s + (−0.401 + 0.915i)3-s + (−0.926 + 0.376i)4-s + (−0.716 + 0.697i)5-s + (−0.975 − 0.218i)6-s + (−0.546 − 0.837i)8-s + (−0.677 − 0.735i)9-s + (−0.821 − 0.569i)10-s + (0.975 + 0.218i)11-s + (0.0275 − 0.999i)12-s + (0.993 − 0.110i)13-s + (−0.350 − 0.936i)15-s + (0.716 − 0.697i)16-s + (−0.789 + 0.614i)17-s + (0.592 − 0.805i)18-s + ⋯
L(s)  = 1  + (0.191 + 0.981i)2-s + (−0.401 + 0.915i)3-s + (−0.926 + 0.376i)4-s + (−0.716 + 0.697i)5-s + (−0.975 − 0.218i)6-s + (−0.546 − 0.837i)8-s + (−0.677 − 0.735i)9-s + (−0.821 − 0.569i)10-s + (0.975 + 0.218i)11-s + (0.0275 − 0.999i)12-s + (0.993 − 0.110i)13-s + (−0.350 − 0.936i)15-s + (0.716 − 0.697i)16-s + (−0.789 + 0.614i)17-s + (0.592 − 0.805i)18-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2527 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.994 - 0.104i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2527 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.994 - 0.104i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(2527\)    =    \(7 \cdot 19^{2}\)
Sign: $-0.994 - 0.104i$
Analytic conductor: \(11.7353\)
Root analytic conductor: \(11.7353\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2527} (31, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 2527,\ (0:\ ),\ -0.994 - 0.104i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(-0.05954460781 + 1.133203274i\)
\(L(\frac12)\) \(\approx\) \(-0.05954460781 + 1.133203274i\)
\(L(1)\) \(\approx\) \(0.5064748079 + 0.7017612079i\)
\(L(1)\) \(\approx\) \(0.5064748079 + 0.7017612079i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad7 \( 1 \)
19 \( 1 \)
good2 \( 1 + (0.191 + 0.981i)T \)
3 \( 1 + (-0.401 + 0.915i)T \)
5 \( 1 + (-0.716 + 0.697i)T \)
11 \( 1 + (0.975 + 0.218i)T \)
13 \( 1 + (0.993 - 0.110i)T \)
17 \( 1 + (-0.789 + 0.614i)T \)
23 \( 1 + (-0.401 - 0.915i)T \)
29 \( 1 + (0.926 + 0.376i)T \)
31 \( 1 + (-0.754 - 0.656i)T \)
37 \( 1 + (0.298 + 0.954i)T \)
41 \( 1 + (0.635 - 0.771i)T \)
43 \( 1 + (0.904 + 0.426i)T \)
47 \( 1 + (0.677 - 0.735i)T \)
53 \( 1 + (0.298 + 0.954i)T \)
59 \( 1 + (-0.986 - 0.164i)T \)
61 \( 1 + (-0.546 + 0.837i)T \)
67 \( 1 + (0.998 - 0.0550i)T \)
71 \( 1 + (0.998 - 0.0550i)T \)
73 \( 1 + (-0.789 + 0.614i)T \)
79 \( 1 + (0.821 - 0.569i)T \)
83 \( 1 + (-0.245 + 0.969i)T \)
89 \( 1 + (0.789 + 0.614i)T \)
97 \( 1 + (0.451 + 0.892i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

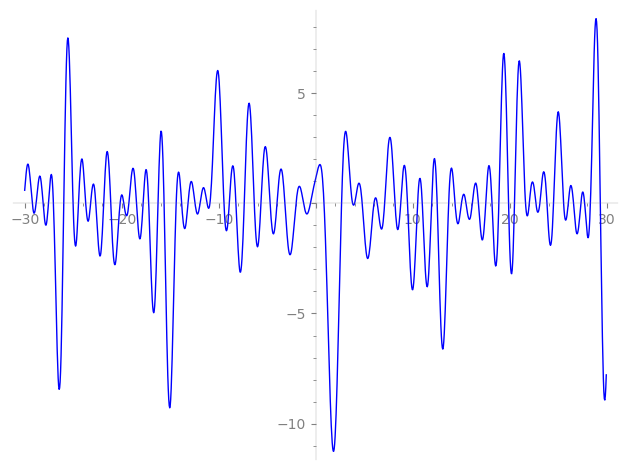
Imaginary part of the first few zeros on the critical line

−19.258763799197801460435330631117, −18.475080840333345754482817217044, −17.78902562715851507212001794524, −17.21724657345876713087403362055, −16.25800854775041483407908262210, −15.63062453642996268431552194106, −14.38520910596235113974199322798, −13.82318839855604810599945901424, −13.16564425074262870113663839527, −12.44579069105605959416811216222, −11.91524733900256103223521384905, −11.20347175571508179191013684679, −10.903003696121148146462431058, −9.45835408870835635802104142384, −8.90998727605182708294609621646, −8.22340471662580031448258150475, −7.368619539024977349194237386891, −6.33594828543056845342209480540, −5.64356642344260038794392069862, −4.707489986070229352297106554932, −3.988459361940876129930303502558, −3.177341462036063544107651512899, −2.030641588333981724510024313886, −1.25817544661278093446883171188, −0.54411214144878532590394471312, 0.85356874771473367993037002423, 2.66355522267855863921662719170, 3.797993264353329322824960473, 4.009011664104945691863181827742, 4.78861849614633928062880597359, 6.00417163697732621413780682114, 6.33920810541188264513739730518, 7.10603257167282139766899369861, 8.167084138322934169646263083468, 8.76290443344995433481883859359, 9.46090973327157492095207277258, 10.50123403677323611894185082766, 10.98274920497243461108280238434, 11.94229140781881972894845265127, 12.51841561350811801107161190607, 13.70321082091211415872970989721, 14.35675446960629413226749496837, 15.01954612377290675706180751369, 15.49159451424018580549687861828, 16.145006642205385387388110423548, 16.77279002207924309733787308297, 17.52646216566847317806020952378, 18.16983948450151538587780591732, 18.87753489993039610819467339692, 19.874797913797908136370129618839

Graph of the $Z$-function along the critical line