↑

Properties

Label 1-15e2-225.203-r0-0-0
Degree $1$
Conductor $225$
Sign $-0.747 + 0.663i$
Analytic cond. $1.04489$
Root an. cond. $1.04489$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.406 + 0.913i)2-s + (−0.669 + 0.743i)4-s + (0.866 + 0.5i)7-s + (−0.951 − 0.309i)8-s + (−0.913 + 0.406i)11-s + (−0.406 + 0.913i)13-s + (−0.104 + 0.994i)14-s + (−0.104 − 0.994i)16-s + (0.951 + 0.309i)17-s + (−0.309 + 0.951i)19-s + (−0.743 − 0.669i)22-s + (0.994 + 0.104i)23-s − 26-s + (−0.951 + 0.309i)28-s + (−0.978 − 0.207i)29-s + ⋯
L(s)  = 1  + (0.406 + 0.913i)2-s + (−0.669 + 0.743i)4-s + (0.866 + 0.5i)7-s + (−0.951 − 0.309i)8-s + (−0.913 + 0.406i)11-s + (−0.406 + 0.913i)13-s + (−0.104 + 0.994i)14-s + (−0.104 − 0.994i)16-s + (0.951 + 0.309i)17-s + (−0.309 + 0.951i)19-s + (−0.743 − 0.669i)22-s + (0.994 + 0.104i)23-s − 26-s + (−0.951 + 0.309i)28-s + (−0.978 − 0.207i)29-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 225 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.747 + 0.663i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 225 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.747 + 0.663i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(225\)    =    \(3^{2} \cdot 5^{2}\)
Sign: $-0.747 + 0.663i$
Analytic conductor: \(1.04489\)
Root analytic conductor: \(1.04489\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{225} (203, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 225,\ (0:\ ),\ -0.747 + 0.663i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.4500607980 + 1.184793412i\)
\(L(\frac12)\) \(\approx\) \(0.4500607980 + 1.184793412i\)
\(L(1)\) \(\approx\) \(0.8809857208 + 0.7786467736i\)
\(L(1)\) \(\approx\) \(0.8809857208 + 0.7786467736i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 \)
5 \( 1 \)
good2 \( 1 + (0.406 + 0.913i)T \)
7 \( 1 + (0.866 + 0.5i)T \)
11 \( 1 + (-0.913 + 0.406i)T \)
13 \( 1 + (-0.406 + 0.913i)T \)
17 \( 1 + (0.951 + 0.309i)T \)
19 \( 1 + (-0.309 + 0.951i)T \)
23 \( 1 + (0.994 + 0.104i)T \)
29 \( 1 + (-0.978 - 0.207i)T \)
31 \( 1 + (-0.978 + 0.207i)T \)
37 \( 1 + (0.587 + 0.809i)T \)
41 \( 1 + (-0.913 - 0.406i)T \)
43 \( 1 + (-0.866 - 0.5i)T \)
47 \( 1 + (0.207 - 0.978i)T \)
53 \( 1 + (0.951 - 0.309i)T \)
59 \( 1 + (0.913 + 0.406i)T \)
61 \( 1 + (0.913 - 0.406i)T \)
67 \( 1 + (0.207 + 0.978i)T \)
71 \( 1 + (-0.309 - 0.951i)T \)
73 \( 1 + (0.587 - 0.809i)T \)
79 \( 1 + (0.978 + 0.207i)T \)
83 \( 1 + (0.743 - 0.669i)T \)
89 \( 1 + (-0.809 - 0.587i)T \)
97 \( 1 + (-0.207 + 0.978i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

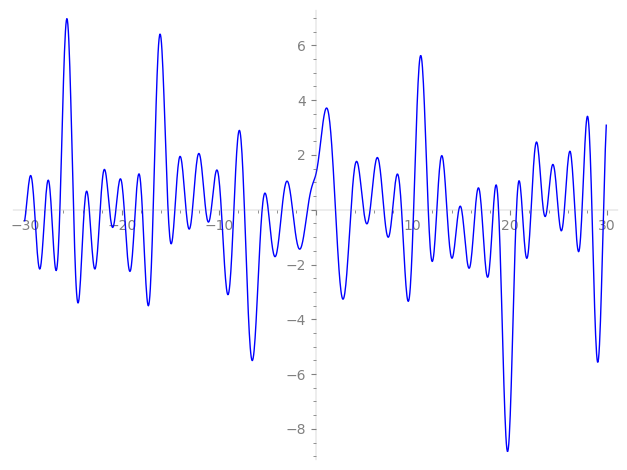
Imaginary part of the first few zeros on the critical line

−26.37278461262415301498278162222, −24.96496009754133890923314779075, −23.86492332457266228556534044968, −23.34162791195069523780303257902, −22.221303716759815244850898679658, −21.25529211420520639033789544235, −20.59889566534220799389265952955, −19.73606407060887215859416072128, −18.600617746301114474231430387106, −17.86945117302264049519102355648, −16.755138776087998471508940411471, −15.22238543661159548638201716803, −14.51919016502322134353213946095, −13.36877261923359836402675622831, −12.70658435808159523705307895562, −11.339778347911059948355440819958, −10.77135058783663772346249627825, −9.73060410118388156548006452025, −8.43759409059797953642466531030, −7.34616464005494957565670360151, −5.52509314159753548944743362121, −4.89443362333168054195437818014, −3.49086780493879760275277932732, −2.38836552818230153558639360911, −0.84717317523910561205296241896, 2.03799317154320998875827753113, 3.63477640633816729806546689274, 4.93236206940132882777325046876, 5.60665960038225075159013014931, 7.02964148249484958709885171409, 7.91998112922845220548380249164, 8.84639780505649539364337549026, 10.09141171196879688815414500186, 11.60037624856020752946499426372, 12.484390100798713152316225271794, 13.524169597249366555481015639147, 14.74760916212402484272690113547, 15.04088492485954916823957556124, 16.44182024844910074557647400032, 17.09074333592179855156889330004, 18.30444954404643180651905586768, 18.84665130932630441435730102807, 20.6921517601030938371256444529, 21.28527355161519898681346834377, 22.20119218328173176923714486556, 23.46368840569615115628783496381, 23.835083837068841565901339574884, 24.99390856370536253654487853309, 25.630375181736223903133159445899, 26.705706468556564332305654349787

Graph of the $Z$-function along the critical line