↑

Properties

Label 1-1392-1392.299-r0-0-0
Degree $1$
Conductor $1392$
Sign $-0.672 + 0.740i$
Analytic cond. $6.46442$
Root an. cond. $6.46442$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.781 − 0.623i)5-s + (−0.222 + 0.974i)7-s + (0.433 + 0.900i)11-s + (0.433 + 0.900i)13-s + 17-s + (−0.974 + 0.222i)19-s + (−0.623 − 0.781i)23-s + (0.222 + 0.974i)25-s + (0.623 − 0.781i)31-s + (0.781 − 0.623i)35-s + (−0.433 + 0.900i)37-s − 41-s + (−0.781 + 0.623i)43-s + (0.900 − 0.433i)47-s + (−0.900 − 0.433i)49-s + ⋯
L(s)  = 1  + (−0.781 − 0.623i)5-s + (−0.222 + 0.974i)7-s + (0.433 + 0.900i)11-s + (0.433 + 0.900i)13-s + 17-s + (−0.974 + 0.222i)19-s + (−0.623 − 0.781i)23-s + (0.222 + 0.974i)25-s + (0.623 − 0.781i)31-s + (0.781 − 0.623i)35-s + (−0.433 + 0.900i)37-s − 41-s + (−0.781 + 0.623i)43-s + (0.900 − 0.433i)47-s + (−0.900 − 0.433i)49-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1392 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.672 + 0.740i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1392 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.672 + 0.740i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(1392\)    =    \(2^{4} \cdot 3 \cdot 29\)
Sign: $-0.672 + 0.740i$
Analytic conductor: \(6.46442\)
Root analytic conductor: \(6.46442\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1392} (299, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 1392,\ (0:\ ),\ -0.672 + 0.740i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.2964851579 + 0.6699264747i\)
\(L(\frac12)\) \(\approx\) \(0.2964851579 + 0.6699264747i\)
\(L(1)\) \(\approx\) \(0.8062093470 + 0.1756438560i\)
\(L(1)\) \(\approx\) \(0.8062093470 + 0.1756438560i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
3 \( 1 \)
29 \( 1 \)
good5 \( 1 + (-0.781 - 0.623i)T \)
7 \( 1 + (-0.222 + 0.974i)T \)
11 \( 1 + (0.433 + 0.900i)T \)
13 \( 1 + (0.433 + 0.900i)T \)
17 \( 1 + T \)
19 \( 1 + (-0.974 + 0.222i)T \)
23 \( 1 + (-0.623 - 0.781i)T \)
31 \( 1 + (0.623 - 0.781i)T \)
37 \( 1 + (-0.433 + 0.900i)T \)
41 \( 1 - T \)
43 \( 1 + (-0.781 + 0.623i)T \)
47 \( 1 + (0.900 - 0.433i)T \)
53 \( 1 + (-0.781 - 0.623i)T \)
59 \( 1 - iT \)
61 \( 1 + (-0.974 - 0.222i)T \)
67 \( 1 + (0.433 - 0.900i)T \)
71 \( 1 + (0.900 - 0.433i)T \)
73 \( 1 + (0.623 + 0.781i)T \)
79 \( 1 + (-0.900 - 0.433i)T \)
83 \( 1 + (-0.974 + 0.222i)T \)
89 \( 1 + (-0.623 + 0.781i)T \)
97 \( 1 + (0.222 + 0.974i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

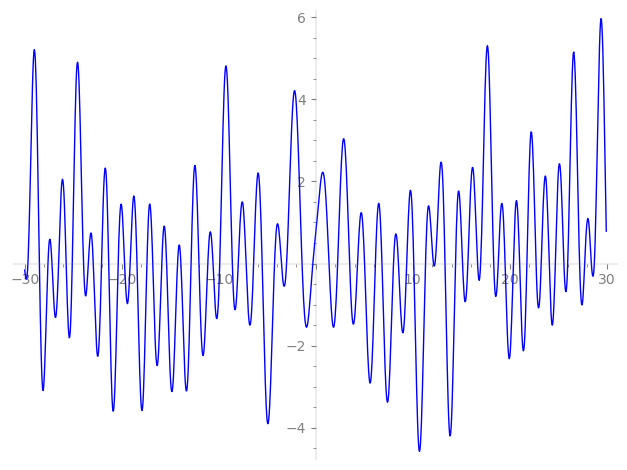
Imaginary part of the first few zeros on the critical line

−20.366831797281980411667776286686, −19.70464371506496435724937454747, −19.12932242590377613368765080131, −18.42214914080223218134354701353, −17.401543306528754601414906355451, −16.79722228604257912229812809664, −15.871886315243217057780725332330, −15.3684739837341262375085191089, −14.24634183193787017947811879300, −13.89452341151951825942706362617, −12.84953127304824307034965470719, −12.035912339460628123366192356995, −11.12568690122733507205167559552, −10.58524141449753819958269965427, −9.894304723445224168092085541248, −8.59744710033764859614913583707, −7.98760628963782852067977721802, −7.17754521515802957508506921496, −6.40138593132216770032608479912, −5.52211927792669182867786738189, −4.248741461313379288885333062644, −3.53496669713517103353800400855, −3.00316786606595717740177977647, −1.41045150716773246554524235911, −0.29827583061007801013602696580, 1.371534422272910473523081030603, 2.25938736160847729691419618897, 3.49199910544838140626850555387, 4.31147806673715675670100626047, 5.03546761411902006896026668569, 6.14808614947841717707716048323, 6.82888905252633543802155335152, 8.01654365849715031070544516605, 8.52764224484786480736678991873, 9.37782868228095831474032048289, 10.10719441274346379977036021007, 11.31263144574561384596532030360, 12.139343885808311052780946849433, 12.30012325861868824738625006843, 13.32918160666268784111737171762, 14.40026666319018644921202223415, 15.13442108095035478827634090345, 15.68404722587069803021149026244, 16.67988655805180214260707632591, 16.99914439061423052117911757443, 18.34748335722527069287079891043, 18.81424358596675125616153898977, 19.51937529157729021900311316249, 20.37172901327591434577930004308, 21.01899510076756564274373869027

Graph of the $Z$-function along the critical line