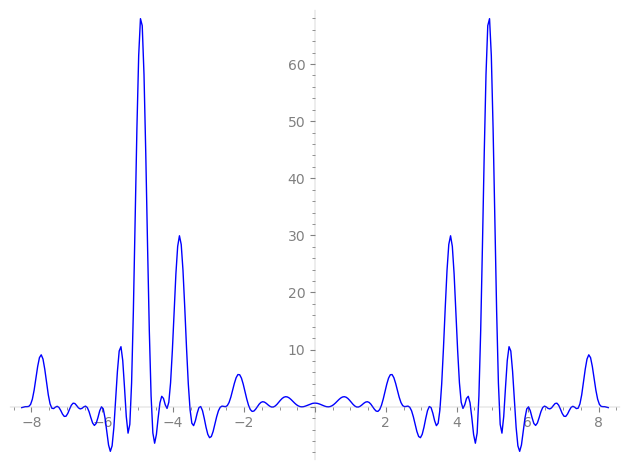
| L(s) = 1 | − 3·2-s + 6·4-s − 3·7-s − 10·8-s + 3·11-s + 9·14-s + 15·16-s − 9·17-s + 6·19-s − 9·22-s − 2·27-s − 18·28-s − 9·29-s + 15·31-s − 21·32-s + 27·34-s + 12·37-s − 18·38-s + 6·41-s − 12·43-s + 18·44-s + 3·47-s − 6·49-s − 9·53-s + 6·54-s + 30·56-s + 27·58-s + ⋯ |
| L(s) = 1 | − 2.12·2-s + 3·4-s − 1.13·7-s − 3.53·8-s + 0.904·11-s + 2.40·14-s + 15/4·16-s − 2.18·17-s + 1.37·19-s − 1.91·22-s − 0.384·27-s − 3.40·28-s − 1.67·29-s + 2.69·31-s − 3.71·32-s + 4.63·34-s + 1.97·37-s − 2.91·38-s + 0.937·41-s − 1.82·43-s + 2.71·44-s + 0.437·47-s − 6/7·49-s − 1.23·53-s + 0.816·54-s + 4.00·56-s + 3.54·58-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{3} \cdot 5^{6} \cdot 13^{6}\right)^{s/2} \, \Gamma_{\C}(s)^{3} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{3} \cdot 5^{6} \cdot 13^{6}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{3} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(0.6217328498\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.6217328498\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_1$ | \( ( 1 + T )^{3} \) |
| 5 | | \( 1 \) |
| 13 | | \( 1 \) |
| good | 3 | $D_{6}$ | \( 1 + 2 T^{3} + p^{3} T^{6} \) |
| 7 | $S_4\times C_2$ | \( 1 + 3 T + 15 T^{2} + 36 T^{3} + 15 p T^{4} + 3 p^{2} T^{5} + p^{3} T^{6} \) |
| 11 | $S_4\times C_2$ | \( 1 - 3 T + 6 T^{2} - 21 T^{3} + 6 p T^{4} - 3 p^{2} T^{5} + p^{3} T^{6} \) |
| 17 | $C_2$ | \( ( 1 + 3 T + p T^{2} )^{3} \) |
| 19 | $S_4\times C_2$ | \( 1 - 6 T + 60 T^{2} - 216 T^{3} + 60 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 23 | $S_4\times C_2$ | \( 1 + 27 T^{2} - 24 T^{3} + 27 p T^{4} + p^{3} T^{6} \) |
| 29 | $S_4\times C_2$ | \( 1 + 9 T + 63 T^{2} + 282 T^{3} + 63 p T^{4} + 9 p^{2} T^{5} + p^{3} T^{6} \) |
| 31 | $S_4\times C_2$ | \( 1 - 15 T + 141 T^{2} - 870 T^{3} + 141 p T^{4} - 15 p^{2} T^{5} + p^{3} T^{6} \) |
| 37 | $S_4\times C_2$ | \( 1 - 12 T + 129 T^{2} - 816 T^{3} + 129 p T^{4} - 12 p^{2} T^{5} + p^{3} T^{6} \) |
| 41 | $S_4\times C_2$ | \( 1 - 6 T + 60 T^{2} - 132 T^{3} + 60 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 43 | $C_2$ | \( ( 1 + 4 T + p T^{2} )^{3} \) |
| 47 | $S_4\times C_2$ | \( 1 - 3 T + 69 T^{2} - 426 T^{3} + 69 p T^{4} - 3 p^{2} T^{5} + p^{3} T^{6} \) |
| 53 | $S_4\times C_2$ | \( 1 + 9 T + 135 T^{2} + 942 T^{3} + 135 p T^{4} + 9 p^{2} T^{5} + p^{3} T^{6} \) |
| 59 | $S_4\times C_2$ | \( 1 - 15 T + 105 T^{2} - 546 T^{3} + 105 p T^{4} - 15 p^{2} T^{5} + p^{3} T^{6} \) |
| 61 | $S_4\times C_2$ | \( 1 + 15 T + 177 T^{2} + 1604 T^{3} + 177 p T^{4} + 15 p^{2} T^{5} + p^{3} T^{6} \) |
| 67 | $S_4\times C_2$ | \( 1 - 9 T + 186 T^{2} - 1083 T^{3} + 186 p T^{4} - 9 p^{2} T^{5} + p^{3} T^{6} \) |
| 71 | $C_2$ | \( ( 1 + p T^{2} )^{3} \) |
| 73 | $S_4\times C_2$ | \( 1 - 6 T + 84 T^{2} + 24 T^{3} + 84 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6} \) |
| 79 | $S_4\times C_2$ | \( 1 + 18 T + 315 T^{2} + 2864 T^{3} + 315 p T^{4} + 18 p^{2} T^{5} + p^{3} T^{6} \) |
| 83 | $S_4\times C_2$ | \( 1 + 15 T + 294 T^{2} + 2481 T^{3} + 294 p T^{4} + 15 p^{2} T^{5} + p^{3} T^{6} \) |
| 89 | $S_4\times C_2$ | \( 1 + 24 T + 384 T^{2} + 3966 T^{3} + 384 p T^{4} + 24 p^{2} T^{5} + p^{3} T^{6} \) |
| 97 | $S_4\times C_2$ | \( 1 + 30 T + 555 T^{2} + 6444 T^{3} + 555 p T^{4} + 30 p^{2} T^{5} + p^{3} T^{6} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{6} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.89583484843580398729790317457, −6.70261721324341612239964172614, −6.51635611496160342127726239265, −6.44371088474770202355271296893, −6.01574802273266631100159662934, −6.01293748468393471241139130545, −5.63645376623594353948143883805, −5.34308535044683439151861804235, −5.19859754487782953873703600785, −4.61386001058717616359999864607, −4.39021985516740310295793355322, −4.20915087562386301009816096698, −4.14822030574746653063806936638, −3.53237837229887731391358510950, −3.25852880033337233422968655529, −3.22110246684752408933198903503, −2.65827374142801969685897406633, −2.53878819120080944812582324230, −2.52538679438836504537096635274, −1.86197238039665732481560289652, −1.62611692358945464710492520605, −1.25420877052718027038594773668, −1.15184606277012740608968091174, −0.41635239379357541054152998322, −0.32299476978437139009691436830,
0.32299476978437139009691436830, 0.41635239379357541054152998322, 1.15184606277012740608968091174, 1.25420877052718027038594773668, 1.62611692358945464710492520605, 1.86197238039665732481560289652, 2.52538679438836504537096635274, 2.53878819120080944812582324230, 2.65827374142801969685897406633, 3.22110246684752408933198903503, 3.25852880033337233422968655529, 3.53237837229887731391358510950, 4.14822030574746653063806936638, 4.20915087562386301009816096698, 4.39021985516740310295793355322, 4.61386001058717616359999864607, 5.19859754487782953873703600785, 5.34308535044683439151861804235, 5.63645376623594353948143883805, 6.01293748468393471241139130545, 6.01574802273266631100159662934, 6.44371088474770202355271296893, 6.51635611496160342127726239265, 6.70261721324341612239964172614, 6.89583484843580398729790317457