| L(s) = 1 | − 3-s − 3·5-s − 4·7-s + 3·9-s − 3·11-s + 3·15-s − 9·17-s − 7·19-s + 4·21-s − 15·23-s + 25-s − 8·27-s + 12·29-s + 5·31-s + 3·33-s + 12·35-s − 5·37-s − 9·45-s + 3·47-s + 9·49-s + 9·51-s − 9·53-s + 9·55-s + 7·57-s − 9·59-s − 15·61-s − 12·63-s + ⋯ |
| L(s) = 1 | − 0.577·3-s − 1.34·5-s − 1.51·7-s + 9-s − 0.904·11-s + 0.774·15-s − 2.18·17-s − 1.60·19-s + 0.872·21-s − 3.12·23-s + 1/5·25-s − 1.53·27-s + 2.22·29-s + 0.898·31-s + 0.522·33-s + 2.02·35-s − 0.821·37-s − 1.34·45-s + 0.437·47-s + 9/7·49-s + 1.26·51-s − 1.23·53-s + 1.21·55-s + 0.927·57-s − 1.17·59-s − 1.92·61-s − 1.51·63-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 200704 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 200704 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | | \( 1 \) |
| 7 | $C_2$ | \( 1 + 4 T + p T^{2} \) |
| good | 3 | $C_2^2$ | \( 1 + T - 2 T^{2} + p T^{3} + p^{2} T^{4} \) |
| 5 | $C_2^2$ | \( 1 + 3 T + 8 T^{2} + 3 p T^{3} + p^{2} T^{4} \) |
| 11 | $C_2^2$ | \( 1 + 3 T + 14 T^{2} + 3 p T^{3} + p^{2} T^{4} \) |
| 13 | $C_2$ | \( ( 1 - p T^{2} )^{2} \) |
| 17 | $C_2^2$ | \( 1 + 9 T + 44 T^{2} + 9 p T^{3} + p^{2} T^{4} \) |
| 19 | $C_2$ | \( ( 1 - T + p T^{2} )( 1 + 8 T + p T^{2} ) \) |
| 23 | $C_2^2$ | \( 1 + 15 T + 98 T^{2} + 15 p T^{3} + p^{2} T^{4} \) |
| 29 | $C_2$ | \( ( 1 - 6 T + p T^{2} )^{2} \) |
| 31 | $C_2^2$ | \( 1 - 5 T - 6 T^{2} - 5 p T^{3} + p^{2} T^{4} \) |
| 37 | $C_2^2$ | \( 1 + 5 T - 12 T^{2} + 5 p T^{3} + p^{2} T^{4} \) |
| 41 | $C_2^2$ | \( 1 - 34 T^{2} + p^{2} T^{4} \) |
| 43 | $C_2^2$ | \( 1 - 74 T^{2} + p^{2} T^{4} \) |
| 47 | $C_2^2$ | \( 1 - 3 T - 38 T^{2} - 3 p T^{3} + p^{2} T^{4} \) |
| 53 | $C_2^2$ | \( 1 + 9 T + 28 T^{2} + 9 p T^{3} + p^{2} T^{4} \) |
| 59 | $C_2^2$ | \( 1 + 9 T + 22 T^{2} + 9 p T^{3} + p^{2} T^{4} \) |
| 61 | $C_2$ | \( ( 1 + T + p T^{2} )( 1 + 14 T + p T^{2} ) \) |
| 67 | $C_2^2$ | \( 1 - 9 T + 94 T^{2} - 9 p T^{3} + p^{2} T^{4} \) |
| 71 | $C_2^2$ | \( 1 - 130 T^{2} + p^{2} T^{4} \) |
| 73 | $C_2$ | \( ( 1 - 10 T + p T^{2} )( 1 + 7 T + p T^{2} ) \) |
| 79 | $C_2$ | \( ( 1 - 13 T + p T^{2} )( 1 + 4 T + p T^{2} ) \) |
| 83 | $C_2$ | \( ( 1 - 12 T + p T^{2} )^{2} \) |
| 89 | $C_2^2$ | \( 1 + 21 T + 236 T^{2} + 21 p T^{3} + p^{2} T^{4} \) |
| 97 | $C_2^2$ | \( 1 - 146 T^{2} + p^{2} T^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
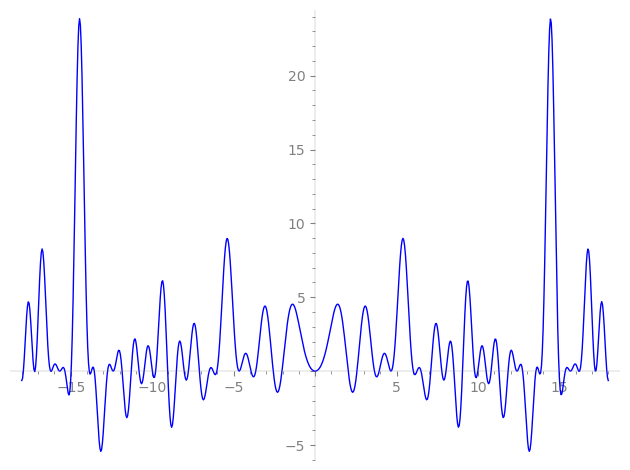
Imaginary part of the first few zeros on the critical line
−10.80360376679959592886162014842, −10.49634388134622438449678127577, −9.986530660529737731576087840904, −9.786471762417294322560496695438, −9.048066061743774172803231474715, −8.518696948733025503913910717939, −8.035291983805885900797018664265, −7.77707565756563504529259897404, −7.10175136180396577909991532483, −6.50166210010701966268844650300, −6.25344521157149162080823110883, −6.02925312566796525387951620130, −4.66231159497816068174300906934, −4.65965766850904310045235773508, −3.93210623899632989845404492968, −3.64271175052699327714804948434, −2.56847658675396888151450917094, −2.03280589619130762961777842844, 0, 0,
2.03280589619130762961777842844, 2.56847658675396888151450917094, 3.64271175052699327714804948434, 3.93210623899632989845404492968, 4.65965766850904310045235773508, 4.66231159497816068174300906934, 6.02925312566796525387951620130, 6.25344521157149162080823110883, 6.50166210010701966268844650300, 7.10175136180396577909991532483, 7.77707565756563504529259897404, 8.035291983805885900797018664265, 8.518696948733025503913910717939, 9.048066061743774172803231474715, 9.786471762417294322560496695438, 9.986530660529737731576087840904, 10.49634388134622438449678127577, 10.80360376679959592886162014842