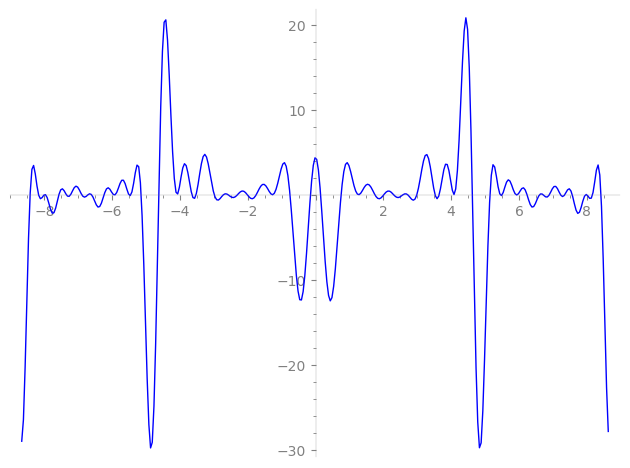
| L(s) = 1 | + 112·4-s + 7.36e3·16-s − 7.20e3·25-s + 812·37-s + 1.87e4·43-s + 3.58e5·64-s + 1.20e5·67-s − 1.57e5·79-s − 8.07e5·100-s − 8.26e5·109-s − 2.49e4·121-s + 127-s + 131-s + 137-s + 139-s + 9.09e4·148-s + 149-s + 151-s + 157-s + 163-s + 167-s − 1.16e6·169-s + 2.10e6·172-s + 173-s + 179-s + 181-s + 191-s + ⋯ |
| L(s) = 1 | + 7/2·4-s + 7.18·16-s − 2.30·25-s + 0.0975·37-s + 1.54·43-s + 10.9·64-s + 3.28·67-s − 2.84·79-s − 8.07·100-s − 6.66·109-s − 0.154·121-s + 5.50e−6·127-s + 5.09e−6·131-s + 4.55e−6·137-s + 4.38e−6·139-s + 0.341·148-s + 3.69e−6·149-s + 3.56e−6·151-s + 3.23e−6·157-s + 2.94e−6·163-s + 2.77e−6·167-s − 3.14·169-s + 5.42·172-s + 2.54e−6·173-s + 2.33e−6·179-s + 2.26e−6·181-s + 1.98e−6·191-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{8} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(6-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{8} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s+5/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(3)\) |
\(\approx\) |
\(4.387039112\) |
| \(L(\frac12)\) |
\(\approx\) |
\(4.387039112\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 3 | | \( 1 \) |
| 7 | | \( 1 \) |
| good | 2 | $C_2^2$ | \( ( 1 - 7 p^{3} T^{2} + p^{10} T^{4} )^{2} \) |
| 5 | $C_2^2$ | \( ( 1 + 3604 T^{2} + p^{10} T^{4} )^{2} \) |
| 11 | $C_2^2$ | \( ( 1 + 12460 T^{2} + p^{10} T^{4} )^{2} \) |
| 13 | $C_2^2$ | \( ( 1 + 584089 T^{2} + p^{10} T^{4} )^{2} \) |
| 17 | $C_2^2$ | \( ( 1 + 2697418 T^{2} + p^{10} T^{4} )^{2} \) |
| 19 | $C_2^2$ | \( ( 1 - 1946195 T^{2} + p^{10} T^{4} )^{2} \) |
| 23 | $C_2^2$ | \( ( 1 + 8382514 T^{2} + p^{10} T^{4} )^{2} \) |
| 29 | $C_2^2$ | \( ( 1 - 19845266 T^{2} + p^{10} T^{4} )^{2} \) |
| 31 | $C_2^2$ | \( ( 1 - 52117859 T^{2} + p^{10} T^{4} )^{2} \) |
| 37 | $C_2$ | \( ( 1 - 203 T + p^{5} T^{2} )^{4} \) |
| 41 | $C_2^2$ | \( ( 1 + 231705052 T^{2} + p^{10} T^{4} )^{2} \) |
| 43 | $C_2$ | \( ( 1 - 4697 T + p^{5} T^{2} )^{4} \) |
| 47 | $C_2^2$ | \( ( 1 - 116727080 T^{2} + p^{10} T^{4} )^{2} \) |
| 53 | $C_2^2$ | \( ( 1 - 781349954 T^{2} + p^{10} T^{4} )^{2} \) |
| 59 | $C_2^2$ | \( ( 1 + 1405123198 T^{2} + p^{10} T^{4} )^{2} \) |
| 61 | $C_2^2$ | \( ( 1 - 1385219534 T^{2} + p^{10} T^{4} )^{2} \) |
| 67 | $C_2$ | \( ( 1 - 30197 T + p^{5} T^{2} )^{4} \) |
| 71 | $C_2^2$ | \( ( 1 - 3592767500 T^{2} + p^{10} T^{4} )^{2} \) |
| 73 | $C_2^2$ | \( ( 1 - 1301516639 T^{2} + p^{10} T^{4} )^{2} \) |
| 79 | $C_2$ | \( ( 1 + 39385 T + p^{5} T^{2} )^{4} \) |
| 83 | $C_2^2$ | \( ( 1 + 3837977680 T^{2} + p^{10} T^{4} )^{2} \) |
| 89 | $C_2^2$ | \( ( 1 + 62763994 T^{2} + p^{10} T^{4} )^{2} \) |
| 97 | $C_2^2$ | \( ( 1 - 17170432214 T^{2} + p^{10} T^{4} )^{2} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−7.22195220674832965177337714421, −6.89886540446257584069131528741, −6.70455833360453284440412933821, −6.61274152126536380856745338597, −6.23520017098937006706551661418, −5.96321008597775115178918433747, −5.90400914627467593282873625068, −5.50884554000070117412252600126, −5.44223390206349742057369840140, −5.14542435634167089942258351533, −4.62454574620141833145212226422, −4.08689958905320875226658929099, −4.08066114608593548930152815036, −3.64692671653357850429727224918, −3.52347665508884056450203721397, −2.98900578736296688526922740685, −2.70975650112290544812193074253, −2.58933106513905038230819515287, −2.29689719757942935435621367997, −2.01739255479933881249554429201, −1.74710176235442751716154765180, −1.29268769258130562025058400409, −1.24979942629272847968503275083, −0.75468473566835023871698259068, −0.14828463746769552031443452355,
0.14828463746769552031443452355, 0.75468473566835023871698259068, 1.24979942629272847968503275083, 1.29268769258130562025058400409, 1.74710176235442751716154765180, 2.01739255479933881249554429201, 2.29689719757942935435621367997, 2.58933106513905038230819515287, 2.70975650112290544812193074253, 2.98900578736296688526922740685, 3.52347665508884056450203721397, 3.64692671653357850429727224918, 4.08066114608593548930152815036, 4.08689958905320875226658929099, 4.62454574620141833145212226422, 5.14542435634167089942258351533, 5.44223390206349742057369840140, 5.50884554000070117412252600126, 5.90400914627467593282873625068, 5.96321008597775115178918433747, 6.23520017098937006706551661418, 6.61274152126536380856745338597, 6.70455833360453284440412933821, 6.89886540446257584069131528741, 7.22195220674832965177337714421