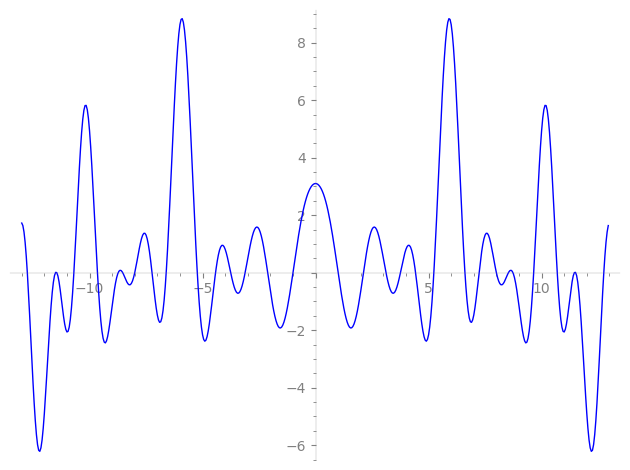
| L(s) = 1 | + 2.52·3-s − 2.85·5-s + 2.52·7-s + 3.38·9-s + 4.85·13-s − 7.21·15-s − 5.61·17-s + 2.52·19-s + 6.38·21-s + 8.17·23-s + 3.14·25-s + 0.964·27-s − 1.38·29-s + 6.61·31-s − 7.21·35-s − 0.618·37-s + 12.2·39-s − 8.61·41-s + 3.12·43-s − 9.65·45-s + 0.596·47-s − 0.618·49-s − 14.1·51-s + 0.381·53-s + 6.38·57-s + 10.7·59-s + 3.61·61-s + ⋯ |
| L(s) = 1 | + 1.45·3-s − 1.27·5-s + 0.954·7-s + 1.12·9-s + 1.34·13-s − 1.86·15-s − 1.36·17-s + 0.579·19-s + 1.39·21-s + 1.70·23-s + 0.629·25-s + 0.185·27-s − 0.256·29-s + 1.18·31-s − 1.21·35-s − 0.101·37-s + 1.96·39-s − 1.34·41-s + 0.476·43-s − 1.43·45-s + 0.0869·47-s − 0.0882·49-s − 1.98·51-s + 0.0524·53-s + 0.845·57-s + 1.39·59-s + 0.463·61-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 3872 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3872 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(3.102625309\) |
| \(L(\frac12)\) |
\(\approx\) |
\(3.102625309\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 \) |
| 11 | \( 1 \) |
| good | 3 | \( 1 - 2.52T + 3T^{2} \) |
| 5 | \( 1 + 2.85T + 5T^{2} \) |
| 7 | \( 1 - 2.52T + 7T^{2} \) |
| 13 | \( 1 - 4.85T + 13T^{2} \) |
| 17 | \( 1 + 5.61T + 17T^{2} \) |
| 19 | \( 1 - 2.52T + 19T^{2} \) |
| 23 | \( 1 - 8.17T + 23T^{2} \) |
| 29 | \( 1 + 1.38T + 29T^{2} \) |
| 31 | \( 1 - 6.61T + 31T^{2} \) |
| 37 | \( 1 + 0.618T + 37T^{2} \) |
| 41 | \( 1 + 8.61T + 41T^{2} \) |
| 43 | \( 1 - 3.12T + 43T^{2} \) |
| 47 | \( 1 - 0.596T + 47T^{2} \) |
| 53 | \( 1 - 0.381T + 53T^{2} \) |
| 59 | \( 1 - 10.7T + 59T^{2} \) |
| 61 | \( 1 - 3.61T + 61T^{2} \) |
| 67 | \( 1 - 13.2T + 67T^{2} \) |
| 71 | \( 1 - 11.6T + 71T^{2} \) |
| 73 | \( 1 + 4.32T + 73T^{2} \) |
| 79 | \( 1 - 3.49T + 79T^{2} \) |
| 83 | \( 1 + 11.6T + 83T^{2} \) |
| 89 | \( 1 + 7.23T + 89T^{2} \) |
| 97 | \( 1 - 17.7T + 97T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.531771129110384752037970856557, −8.000366406748798613163658022749, −7.23408953452136048105789908461, −6.60884025986603985741963141019, −5.23279509936254450856335598505, −4.42510082591747513643490991698, −3.75416973129922506833990620878, −3.11722116546985996867760337725, −2.11866977835498897962020453872, −0.999890994437775815619430851652,
0.999890994437775815619430851652, 2.11866977835498897962020453872, 3.11722116546985996867760337725, 3.75416973129922506833990620878, 4.42510082591747513643490991698, 5.23279509936254450856335598505, 6.60884025986603985741963141019, 7.23408953452136048105789908461, 8.000366406748798613163658022749, 8.531771129110384752037970856557