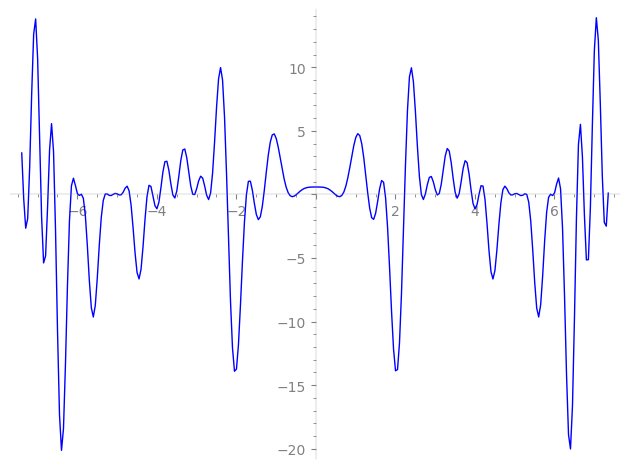
| L(s) = 1 | − 2·4-s − 9-s − 2·13-s + 3·16-s + 2·17-s + 2·36-s + 2·37-s − 2·41-s − 49-s + 4·52-s − 2·53-s − 4·64-s − 4·68-s + 2·73-s + 81-s − 2·113-s + 2·117-s − 121-s + 127-s + 131-s + 137-s + 139-s − 3·144-s − 4·148-s + 149-s + 151-s − 2·153-s + ⋯ |
| L(s) = 1 | − 2·4-s − 9-s − 2·13-s + 3·16-s + 2·17-s + 2·36-s + 2·37-s − 2·41-s − 49-s + 4·52-s − 2·53-s − 4·64-s − 4·68-s + 2·73-s + 81-s − 2·113-s + 2·117-s − 121-s + 127-s + 131-s + 137-s + 139-s − 3·144-s − 4·148-s + 149-s + 151-s − 2·153-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 5^{8} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{8} \cdot 5^{8} \cdot 31^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(0.5831773635\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.5831773635\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ |
|---|
| bad | 2 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| 5 | | \( 1 \) |
| 31 | $C_2$ | \( ( 1 + T^{2} )^{2} \) |
| good | 3 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 7 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 11 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 13 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 17 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 19 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 23 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 29 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 37 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 41 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 43 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 47 | $C_1$$\times$$C_1$ | \( ( 1 - T )^{4}( 1 + T )^{4} \) |
| 53 | $C_1$$\times$$C_2$ | \( ( 1 + T )^{4}( 1 - T + T^{2} )^{2} \) |
| 59 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 61 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 67 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 71 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 73 | $C_1$$\times$$C_2$ | \( ( 1 - T )^{4}( 1 + T + T^{2} )^{2} \) |
| 79 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 83 | $C_2$$\times$$C_2^2$ | \( ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} ) \) |
| 89 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| 97 | $C_2$ | \( ( 1 + T^{2} )^{4} \) |
| show more | | |
| show less | | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−6.16381847990430323535199908533, −5.98715574797049167147782332653, −5.91093858056893490147509846461, −5.88274888478317200341413901089, −5.30304931076906675963313366707, −5.23198607974069209289418157679, −5.09918678045662686728771305503, −4.97143835243241016204739898254, −4.88310409215835416331300301929, −4.68017796430249255503773980469, −4.23970261704306929313984670711, −4.10318184697321885403466354762, −3.91736918097856546598868887130, −3.59981290804783331856514146506, −3.51383858951546843697333741578, −3.09431103325134813198783635849, −3.04412824997628549666527584408, −2.75156659955254892569923343851, −2.65256991078319631942686153038, −2.23037433402858497961219569458, −1.74559645941708754083880639272, −1.58054565546216370193845008479, −1.30814555671626182352958960495, −0.67251071707989783199691988789, −0.48606837205745077532715184452,
0.48606837205745077532715184452, 0.67251071707989783199691988789, 1.30814555671626182352958960495, 1.58054565546216370193845008479, 1.74559645941708754083880639272, 2.23037433402858497961219569458, 2.65256991078319631942686153038, 2.75156659955254892569923343851, 3.04412824997628549666527584408, 3.09431103325134813198783635849, 3.51383858951546843697333741578, 3.59981290804783331856514146506, 3.91736918097856546598868887130, 4.10318184697321885403466354762, 4.23970261704306929313984670711, 4.68017796430249255503773980469, 4.88310409215835416331300301929, 4.97143835243241016204739898254, 5.09918678045662686728771305503, 5.23198607974069209289418157679, 5.30304931076906675963313366707, 5.88274888478317200341413901089, 5.91093858056893490147509846461, 5.98715574797049167147782332653, 6.16381847990430323535199908533